题目内容
17.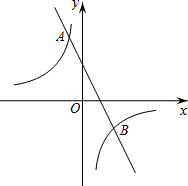 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).(1)求a,m的值;
(2)求该双曲线与直线y=-2x+2另一个交点B的坐标.
分析 (1)将A坐标代入一次函数解析式中即可求得a的值,将A(-1,4)坐标代入反比例解析式中即可求得m的值;
(2)解方程组$\left\{\begin{array}{l}{y=-2x+2}\\{y=\frac{-4}{x}}\end{array}\right.$,即可解答.
解答 解:(1)∵点A的坐标是(-1,a),在直线y=-2x+2上,
∴a=-2×(-1)+2=4,
∴点A的坐标是(-1,4),代入反比例函数y=$\frac{m}{x}$,
∴m=-4.
(2)解方程组$\left\{\begin{array}{l}{y=-2x+2}\\{y=\frac{-4}{x}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$,
∴该双曲线与直线y=-2x+2另一个交点B的坐标为(2,-2).
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:反比例函数的图象上点的坐标特征,待定系数法确定函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在-4,-2,-1,0这四个数中,比-3小的数是( )
| A. | -4 | B. | -2 | C. | -1 | D. | 0 |
 如图,AB∥EF∥CD,点P在线段EF上,当点P从E向F沿线段EF移动时,∠A,∠APC,∠C之间有什么关系?
如图,AB∥EF∥CD,点P在线段EF上,当点P从E向F沿线段EF移动时,∠A,∠APC,∠C之间有什么关系?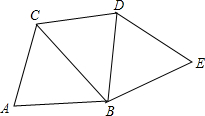 如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
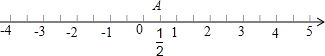 如图,数轴上点A表示$\frac{1}{2}$.
如图,数轴上点A表示$\frac{1}{2}$.