题目内容
8. 如图,AB∥EF∥CD,点P在线段EF上,当点P从E向F沿线段EF移动时,∠A,∠APC,∠C之间有什么关系?
如图,AB∥EF∥CD,点P在线段EF上,当点P从E向F沿线段EF移动时,∠A,∠APC,∠C之间有什么关系?
分析 先分三种情况考虑.根据两直线平行找出相等或互补的角,再依据角的计算得出结论.
解答 解:当点P在AC的左侧时,
∵AB∥EF,
∴∠A+∠APF=180°.
又∵EF∥CD,
∴∠CPF+∠C=180°.
∴∠A+∠APF+∠CPF+∠C=180°+180°=360°,
即∠A+∠C+∠APC=360°;
当点P在AC上时,∠APC=180°,
∵AB∥CD,
∴∠A+∠C=180°,
则∠A+∠C=∠APC=180°;
当点P在AC的右侧时,
∵AB∥EF,
∴∠A=∠APE.
又∵EF∥CD,
∴∠CPE=∠C.
∴∠A+∠C=∠APE+∠CPE,
即∠A+∠C=∠APC.
综上可知:当点P在AC的左侧时,有∠A+∠C+∠APC=360°;当点P在AC上或AC的右侧时,有∠A+∠C=∠APC.
点评 本题考查了平行线的性质,解题的关键是分三种情况考虑.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>5}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<5}\\{x≥-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>5}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<5}\\{x>-1}\end{array}\right.$ |
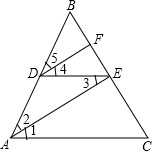 阅读下列推理过程,在括号中填写理由.
阅读下列推理过程,在括号中填写理由.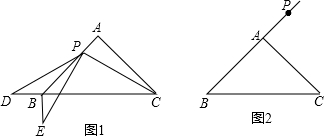
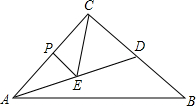 如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,P是AC边上一动点(不与A、C重合),过点P作PE∥BC交AD于点E,将△ABD沿直线AD翻折,得到△AB′D,连接B′C,当∠ACE=∠BCB′时,则AE=$\frac{64}{25}$.
如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,P是AC边上一动点(不与A、C重合),过点P作PE∥BC交AD于点E,将△ABD沿直线AD翻折,得到△AB′D,连接B′C,当∠ACE=∠BCB′时,则AE=$\frac{64}{25}$.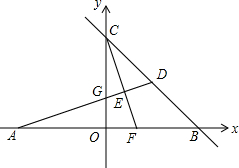 如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.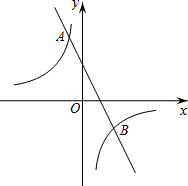 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).