题目内容
12.(1)若$\frac{|x|}{x}$=1,求x.(2)若$\frac{|x|}{x}$=-1,求x.
变式:求$\frac{|x|}{x}$+$\frac{|y|}{y}$的值
变式:$\frac{|x|}{x}$和$\frac{y}{|y|}$互为相反数,求($\frac{|x|}{x}$)2+($\frac{y}{|y|}$)3的值.
分析 (1)由原式得|x|=x,根据绝对值性质得x>0;
(2)由原式得|x|=-x,根据绝对值性质得x<0;
变式:分①x>0,y>0;②x>0,y<0;③x<0,y>0;④x<0,y<0;分别求解可得;
变式:由题意知$\frac{|x|}{x}$+$\frac{y}{|y|}$=0即x、y异号,分①x>0,y<0;②x<0,y>0;两种情况求解.
解答 解:(1)若$\frac{|x|}{x}$=1则x≠0,且|x|=x,即绝对值等于本身,则x是正数;
(2)若$\frac{|x|}{x}$=-1则x≠0,且|x|=-x,即绝对值等于其相反数,则x是负数;
变式:①当x>0,y>0时,$\frac{|x|}{x}$+$\frac{|y|}{y}$=1+1=2;②当x>0,y<0时,$\frac{|x|}{x}$+$\frac{|y|}{y}$=1-1=0;
③当x<0,y>0时,$\frac{|x|}{x}$+$\frac{|y|}{y}$=-1+1=0;④当x<0,y<0时,$\frac{|x|}{x}$+$\frac{|y|}{y}$=-1-1=-2;
综上,$\frac{|x|}{x}$+$\frac{|y|}{y}$的值为±2或0;
变式:根据题意知,$\frac{|x|}{x}$+$\frac{y}{|y|}$=0,
∴x、y异号,
①当x>0,y<0时,($\frac{|x|}{x}$)2+($\frac{y}{|y|}$)3=12+(-1)3=1-1=0;
②当x<0,y>0时,($\frac{|x|}{x}$)2+($\frac{y}{|y|}$)3=(-1)2+13=1+1=2;
综上,($\frac{|x|}{x}$)2+($\frac{y}{|y|}$)3的值为0或2.
点评 本题主要考查绝对值的性质和相反数的性质,根据题意罗列所有情况是解题的关键.

| A. | 中心对称图形 | B. | 对角相等 | C. | 对边平行 | D. | 对角线互相垂直 |
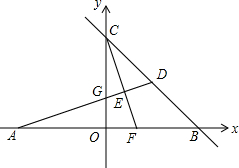 如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.
如图,在平面直角坐标系中,A,B,C为坐标轴上的三点,且OA=OB=OC=4,过点A的直线AD交BC于点D,交y轴于点G,△ABD的面积为8.过点C作CE⊥AD,交AB交于F,垂足为E.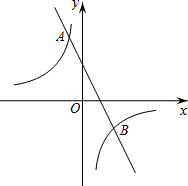 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).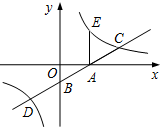 如图,直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
如图,直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$(k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.