题目内容
7.函数y=$\frac{\sqrt{x+3}}{x-5}$中,自变量x的取值范围是x≥-3且x≠5.分析 根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:由题意得,x+3≥0且x-5≠0,
解得x≥-3且x≠5.
故答案为:x≥-3且x≠5.
点评 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
18. 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
 某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )
某个不等式组的解集在数轴上表示如图,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>5}\\{x≥1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<5}\\{x≥-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>5}\\{x>-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<5}\\{x>-1}\end{array}\right.$ |
15.不等式4+2x>0的解集是( )
| A. | 2x>4 | B. | x>2 | C. | x>-2 | D. | x<-2 |
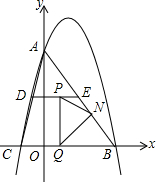 如图,已知抛物线y=-$\frac{4}{3}$x2+bx+c经过A(0,4),B(3,0)两点,与x轴负半轴交于点C,连接AC、AB.
如图,已知抛物线y=-$\frac{4}{3}$x2+bx+c经过A(0,4),B(3,0)两点,与x轴负半轴交于点C,连接AC、AB.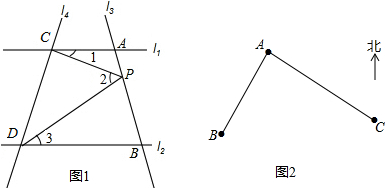
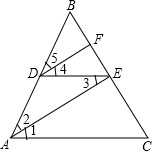 阅读下列推理过程,在括号中填写理由.
阅读下列推理过程,在括号中填写理由.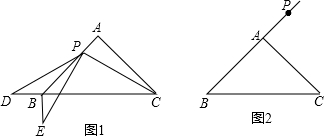
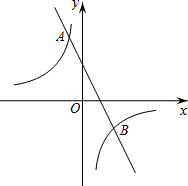 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).