题目内容
13.若关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=-4,则m+n的值是( )| A. | -10 | B. | 10 | C. | -6 | D. | -1 |
分析 结合根与系数的关系可知:“x1+x2=-$\frac{b}{a}$=-m,x1x2=$\frac{c}{a}$=n”,代入x1=2,x2=-4,即可得出m、n的值,从而得出m+n的值.
解答 解:∵关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=2,x2=-4,
∴x1+x2=-$\frac{b}{a}$=-m,x1x2=$\frac{c}{a}$=n,
∴m=2,n=-8,
∴m+n=2-8=-6.
故选C.
点评 本题考查了根与系数的关系,解题的关键是分别求出m、n的值.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出m、n的值是关键.

练习册系列答案
相关题目

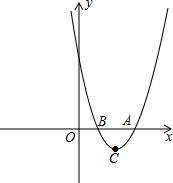 如图,在平面直角坐标系中,抛物线y=x2-4x+3的顶点为C,与x轴交于A、B两点.
如图,在平面直角坐标系中,抛物线y=x2-4x+3的顶点为C,与x轴交于A、B两点.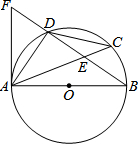 如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE. 如图,△ABC内接于⊙O,∠ACB=20°,则∠BAO=70度.
如图,△ABC内接于⊙O,∠ACB=20°,则∠BAO=70度.