题目内容
14.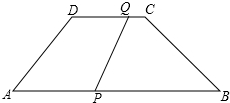 如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.
如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.(1)当t=1.5时,求证:PQ$\stackrel{∥}{=}$AD;
(2)当t=3s时,线段PQ能否平分对角线BD;
(3)当t=$\frac{12}{7}$s时,点P恰好在DQ的垂直平分线上.
分析 (1)先求出AP=DQ,再证明四边形APQD是平行四边形,即可得出结论;
(2)当线段PQ平分对角线BD时,由DE=BE,得出DQ=BP,列出方程,解方程即可;
(3)作DN⊥AB于N,CM⊥AB于M,先求出AN,再由DQ=2PN,列出方程,解方程即可.
解答 解:(1)当t=1.5时,CQ=1.5,AP=3×1.5=4.5,
∴DQ=6-1.5=4.5,
∴AP=DQ,
∵AB∥CD,
∴AP∥DQ,
∴四边形APQD是平行四边形,
∴PQ∥AD,PQ=AD;
(2)当t=3s时,线段PQ能平分对角线BD;
如图所示:连接BD交PQ于E, 理由如下:
理由如下:
∵AB∥CD,
∴BP∥DQ,当线段PQ平分对角线BD时,
∵DE=BE,
∴DQ=BP,
∵DQ=6-t,BP=12-3t,
∴6-t=12-3t,
解得:t=3;
∴当t=3s时,线段PQ能平分对角线BD;
(3)当t=$\frac{12}{7}$s时,点P恰好在DQ的垂直平分线上;理由如下: 如图所示:作DN⊥AB于N,CM⊥AB于M,
如图所示:作DN⊥AB于N,CM⊥AB于M,
则AN=$\frac{1}{2}$(12-6)=3,
当点P恰好在DQ的垂直平分线上时,PF垂直平分DQ,DQ=2PN,
∵PN=3t-3,DQ=6-t,
∴6-t=2(3t-3),
解得:t=$\frac{12}{7}$;
即当t=$\frac{12}{7}$s时,点P恰好在DQ的垂直平分线上.
点评 本题考查了梯形的性质、平行四边形的判定与性质、线段垂直平分线的性质;本题有一定难度,特别是(2)(3)中,需要通过作辅助线,列出方程才能解决问题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
4.已知关于x的方程2x+a-9=0的解是x=2,则a的值为( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
5.若x3=-8,则x的值是( )
| A. | x=-2 | B. | x=2 | C. | x=±2 | D. | 以上都可以 |
3.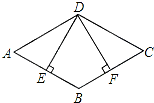 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.| A. | 16$\sqrt{3}$ | B. | 64 | C. | 8$\sqrt{3}$ | D. | 8 |
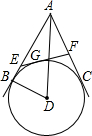 如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.
如图所示,⊙D 的半径为3,A是圆D外一点且AD=5,AB,AC分别与⊙D相切于点B,C.G是劣弧BC上任意一点,过G作⊙D的切线,交AB于点E,交AC于点F.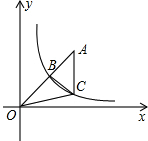 反比例反数y=$\frac{k}{x}$(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=$\frac{k}{x}$(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=4.
反比例反数y=$\frac{k}{x}$(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=$\frac{k}{x}$(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=4. 如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.
如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.