题目内容
6.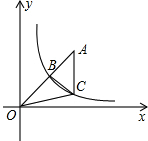 反比例反数y=$\frac{k}{x}$(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=$\frac{k}{x}$(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=4.
反比例反数y=$\frac{k}{x}$(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=$\frac{k}{x}$(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=4.
分析 根据线段中点的性质,可得A点坐标,根据三角形的中线分三角形所得两个三角形的面积相等,可得S△ABC=S△BOC=3,根据反比例函数的定义,可得△COD的面积,根据三角形面积的和差,可得关于k的方程,根据解方程,可得答案.
解答 解:如图:延长AC交x轴于D点,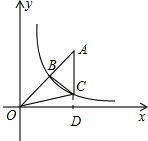
设B点坐标为(a,$\frac{k}{a}$),
由AB=OB,得A(2a,$\frac{2k}{a}$),D(2a,0).
由AB=OB,得S△ABC=S△BOC=3,S△COD=$\frac{1}{2}$OD•CD=$\frac{1}{2}$k.
由三角形面积的和差,得
S△AOD-S△COD=S△AOC,
即$\frac{1}{2}$×2a×$\frac{2k}{a}$-$\frac{1}{2}$k=6.
解得k=4.
故答案为:4.
点评 本题考查了反比例函数k的几何意义,利用了三角形的中线分三角形所得两个三角形的面积相等,利用三角形面积的和差得出关于k的方程是解题关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
1.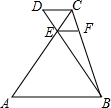 如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
 如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
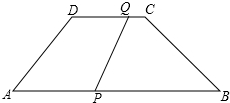 如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.
如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.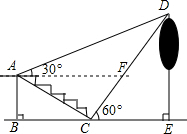 某校数学兴趣小组的同学为了利用所学知识,测量校园内一棵树DE的高度(如图所示),当这棵树顶点D的影子刚好落在旗台的台阶下点C处时,他们测得此时树顶点D的仰角为60°;当点D的影子刚好落在台阶上点A时,树顶点D的仰角为30°,台阶坡度为$\sqrt{3}$:3,台阶高度AB=2米,点B、C、E在同一水平线上,求树高DE(测角仪高度忽略不计).
某校数学兴趣小组的同学为了利用所学知识,测量校园内一棵树DE的高度(如图所示),当这棵树顶点D的影子刚好落在旗台的台阶下点C处时,他们测得此时树顶点D的仰角为60°;当点D的影子刚好落在台阶上点A时,树顶点D的仰角为30°,台阶坡度为$\sqrt{3}$:3,台阶高度AB=2米,点B、C、E在同一水平线上,求树高DE(测角仪高度忽略不计).