题目内容
9.若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.已知四边形ABCD中,AB=AD=BC=2,∠BAD=90°,AC是四边形ABCD的和谐线,且AC≠CD,求四边形ABCD的面积.分析 首先根据题意画出图形,然后由AC是四边形ABCD的和谐线,可以得出△ACD是等腰三角形,从图1,图2两种情况运用等边三角形的性质,正方形的性质和30°的直角三角形性质就可以得出四边形ABCD的面积.
解答 解:如图,
∵AC是四边形ABCD的和谐线,
∴△ACD是等腰三角形.
∵AB=AD=BC,
如图1,当AD=AC时,
∴AB=AC=BC,∠ACD=∠ADC
∴△ABC是正三角形,
∴∠BAC=∠BCA=60°.
∵∠BAD=90°,
∴∠CAD=30°,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$×2×2×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×2×2×$\frac{1}{2}$=$\sqrt{3}$+1.
如图2,当AD=CD时,
∴AB=AD=BC=CD.
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴S四边形ABCD=2×2=4;
综上所知四边形ABCD的面积为$\sqrt{3}$+1或4.
点评 此题考查了等腰三角形的性质、矩形的性质、正方形的性质以及含30°角的直角三角形的性质.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
20.小明用一枚均匀的硬币进行试验,连续抛三次,结果都是正面朝上的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
4. 如图,在平行四边形ABCD中,下列结论一定正确的是( )
如图,在平行四边形ABCD中,下列结论一定正确的是( )
 如图,在平行四边形ABCD中,下列结论一定正确的是( )
如图,在平行四边形ABCD中,下列结论一定正确的是( )| A. | AC⊥BD | B. | ∠A+∠B=180° | C. | AB=AD | D. | ∠A+∠C=180° |
1.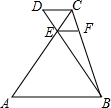 如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
 如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )
如图,AB∥CD∥EF,AC与BD相交于点E,若CE=5,CF=4,AE=BC,则$\frac{CD}{AB}$的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
19. 如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
 如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )
如图,在△ABC中,∠B=67°,∠C=33°,△ABC的角平分线,则∠ADB的度数为( )| A. | 40° | B. | 45° | C. | 73° | D. | 85° |
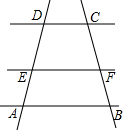 如图,AB∥CD,AB=a,CD=b,点E、F分别在AD、BC上,且EF∥AB,设EF到CD、AB的距离为d1、d2,则有:
如图,AB∥CD,AB=a,CD=b,点E、F分别在AD、BC上,且EF∥AB,设EF到CD、AB的距离为d1、d2,则有: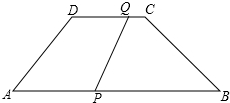 如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.
如图,梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边以1cm/s的速度向D移动,同时点P从A开始沿AB以3cm/s的速度向B移动,当其中一点到达终点时运动停止.设运动时间为t秒.