题目内容
20. 如图,△ABC中,D为BC的中点,
如图,△ABC中,D为BC的中点,(1)在图中作出CM⊥AD,BN⊥AD,垂足分别为M、N;
(z)求证:DM=DN;
(3)求AD=3,求AM+AN的值.
分析 (1)根据条件作出图形,即可解答;
(2)证明△BND≌△CMD,即可得到DN=DM.
(3)由△BND≌△CMD,得到DM=DN,利用线段的和与差得到AM=AD+DM,AN=AD-ND,所以AM+AN=AD+DM+AD-ND=2AD=6.
解答 解:(1)如图,
(2)∵D为BC的中点,
∴BD=CD,
∵CM⊥AD,BN⊥AD,
∴∠BND=∠CMD=90°,
在△BND和△CMD中,
$\left\{\begin{array}{l}{∠BND=∠CMD}\\{∠BDN=∠CDM}\\{BD=CD}\end{array}\right.$
∴△BND≌△CMD,
∴DN=DM.
(3)∵△BND≌△CMD,
∴DM=DN,
∵AM=AD+DM,AN=AD-ND,
∴AM+AN=AD+DM+AD-ND,
∵DM=DN,
∴AM+AN=2AD=6.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△BND≌△CMD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.(-8)2的立方根是( )
| A. | -2 | B. | ±2 | C. | 4 | D. | ±4 |
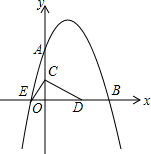 如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.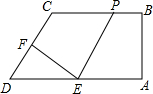 如图,在四边形ABCD中,BC∥AD,∠A=90°,BC<AD,E为AD的中点,F为CD的中点,P是一动点,从点A开始沿AB-BC匀速运动,到达点C即止,记点P运动的时间为x,四边形PEFC的面积为y,y与x关系所反映的图象可能是( )
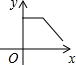
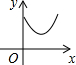
如图,在四边形ABCD中,BC∥AD,∠A=90°,BC<AD,E为AD的中点,F为CD的中点,P是一动点,从点A开始沿AB-BC匀速运动,到达点C即止,记点P运动的时间为x,四边形PEFC的面积为y,y与x关系所反映的图象可能是( )

 如图,点C在线段BE上,在BE的同侧作△ABC和△DCE,AE,BD交于点P,已知AC=BC,DC=EC,∠1=∠2.
如图,点C在线段BE上,在BE的同侧作△ABC和△DCE,AE,BD交于点P,已知AC=BC,DC=EC,∠1=∠2.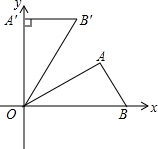 如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°.
如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°. 如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).
如图,边长为$\sqrt{3}$的等边△ABC中,D、E分别为AB、BC上的点,且DB=$\sqrt{2}$,将线段ED绕E点顺时针旋转60°得到线段EF,连CF.当∠FCB=30°时,CE的长为$\frac{1}{2}$($\sqrt{3}$+$\sqrt{2}$).