题目内容
18.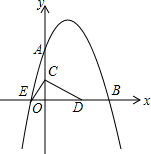 如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
如图,已知抛物线y=-$\frac{1}{2}$x2+bx+c与坐标轴分别交于点点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)求该抛物线的解析式及点E的坐标;
(2)若D点运动的时间为t,△CED的面积为S,求S关于t的函数关系式,并求出△CED的面积的最大值.
分析 (1)将点A(0,8)、B(8,0)代入抛物线y=-$\frac{1}{2}$x2+bx+c即可求出抛物线的解析式为:y=-$\frac{1}{2}$x2+3x+8;再令y=0,得:-$\frac{1}{2}$x2+3x+8=0,解方程可得点E的坐标;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,然后由点A(0,8)、B(8,0),可得OA=8,OB=8,从而可得OD=8-t,然后令y=0,点E的坐标为(-2,0),进而可得OE=2,DE=2+8-t=10-t,然后利用三角形的面积公式即可求△CED的面积S与D点运动时间t的函数解析式为:S=-$\frac{1}{2}$t2+5t,然后转化为顶点式即可求出最值为:S最大=$\frac{25}{2}$.
解答 解:(1)将点A(0,8)、B(8,0)代入抛物线y=-$\frac{1}{2}$x2+bx+c得:$\left\{\begin{array}{l}{c=8}\\{-\frac{1}{2}×64+8b+c=0}\end{array}\right.$,
解得:b=3,c=8,
故抛物线的解析式为:y=-$\frac{1}{2}$x2+3x+8,
∵点A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:-$\frac{1}{2}$x2+3x+8=0,
解得:x1=8,x2=-2,
∵点E在x轴的负半轴上,
∴点E(-2,0),
∴OE=2;
(2)根据题意得:当D点运动t秒时,BD=t,OC=t,
∴OD=8-t,
∴DE=OE+OD=10-t,
∴S=$\frac{1}{2}$•DE•OC=$\frac{1}{2}$•(10-t)•t=-$\frac{1}{2}$t2+5t,
即S=-$\frac{1}{2}$t2+5t=-$\frac{1}{2}$(t-5)2+$\frac{25}{2}$,
∴当t=5时,S最大=$\frac{25}{2}$.
点评 此题考查了二次函数的综合题,解题的关键是熟练以下知识点:用待定系数法求函数关系式,函数的最值问题,三角形的面积公式,综合性较强,难度中等.

| 品种 | 青椒 | 土豆 |
| 批发价(元/kg) | 1.5 | 3 |
| 零售价(元/kg) | 3 | 4 |
(1)第一天,小六批发青椒和土豆两种共200kg,用去了450元钱,这两种蔬菜当天全部售完一共能赚多少元钱?
(2)第二天,还是用去450元钱仍然批发青椒和土豆,要想当天全部售完后所赚钱数不少于270元,则该最多能批发土豆多少kg?
 如图,边长为4cm的正方形ABCD,以点B为圆心、BD为半径画弧与BC边的延长线交于点E,则图中阴影部分的面积为4π-8cm2.
如图,边长为4cm的正方形ABCD,以点B为圆心、BD为半径画弧与BC边的延长线交于点E,则图中阴影部分的面积为4π-8cm2. 如图,AB是半圆O的直径,点C是半圆上的一个动点,∠BAC的角平分线交圆弧于点D,半圆O在点D处的切线与直线AC交于点E.
如图,AB是半圆O的直径,点C是半圆上的一个动点,∠BAC的角平分线交圆弧于点D,半圆O在点D处的切线与直线AC交于点E.

 如图,△ABC中,D为BC的中点,
如图,△ABC中,D为BC的中点, 如图,在△ABC中,∠C=90°,AC=4,AB=5,点P从点A出发,以每秒4个单位长度的速度沿A-C-B运动,到点B时停止.当点P不与△ABC的顶点重合时,过点P作其所在的直角边的垂线,交AB于点Q,再以PQ为斜边作等腰直角三角形△PQR,使点R与△ABC的另一条直角边在PQ的同侧.设点P运动的时间为t(秒).
如图,在△ABC中,∠C=90°,AC=4,AB=5,点P从点A出发,以每秒4个单位长度的速度沿A-C-B运动,到点B时停止.当点P不与△ABC的顶点重合时,过点P作其所在的直角边的垂线,交AB于点Q,再以PQ为斜边作等腰直角三角形△PQR,使点R与△ABC的另一条直角边在PQ的同侧.设点P运动的时间为t(秒).