题目内容
一个袋中装有2个红球,3个白球,和5个黄球,每个球除了顔色外都相同,从中任意摸出一个球,分别求出摸到红球,白球,黄球的概率。
 ,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即
,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
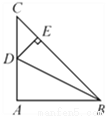
如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan∠DBC 的值为 ( )
A. 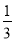 B.
B. 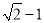 C.
C. 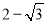 D.
D. 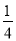
 A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A.
A
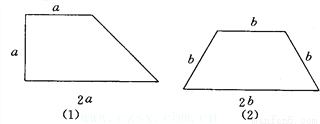
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A. 如图所示,请你把下列梯形分成四个全等的四边形.
 见解析
【解析】试题分析:这两个梯形都是比较特殊的梯形,一个是直角梯形,一个是等腰梯形,因为要分为四个全等的四边形,因此分得的四个四边形与原梯形的形状是一样的,只是各相应的边长变为原来相应边长的一半,据此进行分割即可得.
试题解析:如图所示:
见解析
【解析】试题分析:这两个梯形都是比较特殊的梯形,一个是直角梯形,一个是等腰梯形,因为要分为四个全等的四边形,因此分得的四个四边形与原梯形的形状是一样的,只是各相应的边长变为原来相应边长的一半,据此进行分割即可得.
试题解析:如图所示: 如图,ΔABC≌ΔCDA,∠BAC=∠DCA,则BC的对应边是 ( )
A. CD B. CA C. DA D. AB
 C
【解析】∵ΔABC≌ΔCDA,∠BAC=∠DCA,
∴BC的对应边为DA,
故选C.
C
【解析】∵ΔABC≌ΔCDA,∠BAC=∠DCA,
∴BC的对应边为DA,
故选C. 下列图形能分成两个全等图形的是()
A. 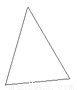
B. 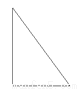
C. 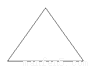
D. 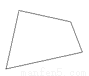
 C
【解析】全等图形需要大小相等,形状相同,原图中只有C是一个等腰三角形可以分成两个全等的直角三角形,A、B、D都不符合要求,
故选C.
C
【解析】全等图形需要大小相等,形状相同,原图中只有C是一个等腰三角形可以分成两个全等的直角三角形,A、B、D都不符合要求,
故选C. 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为__.
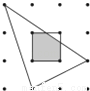
 【解析】试题解析:由题意,中间正方形中直角三角形的面积为,
∴阴影部分的面积为1-,
∴点P落在图中阴影部分的概率是.
【解析】试题解析:由题意,中间正方形中直角三角形的面积为,
∴阴影部分的面积为1-,
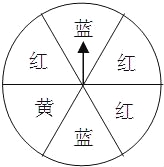
∴点P落在图中阴影部分的概率是. 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A.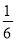 B.
B.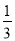 C.
C.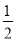 D.
D.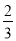
 A
【解析】
试题解析:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率=.
故选A.
A
【解析】
试题解析:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率=.
故选A. 如图,E点为△ABC的边AC的中点,CN∥AB,过E点作直线交AB于M点,交CN于N点,若MB=6cm,CN=4cm,则AB=__cm.
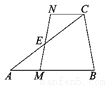
 10
【解析】试题分析:由CN∥AB,可得∠NCE=∠MAE,再结合E是AC中点,对顶角相等,即可证得△CHE≌△MAE,从而得到结果.
∵CN∥AB,
∴∠NCE=∠MAE,
∵E是AC中点,
∴AE=CE,
∵∠AEM=∠CEN,
∴△CHE≌△MAE,
∴AM=CN,
∴AB=AM+BM=CN+BM=4+6=10cm.
10
【解析】试题分析:由CN∥AB,可得∠NCE=∠MAE,再结合E是AC中点,对顶角相等,即可证得△CHE≌△MAE,从而得到结果.
∵CN∥AB,
∴∠NCE=∠MAE,
∵E是AC中点,
∴AE=CE,
∵∠AEM=∠CEN,
∴△CHE≌△MAE,
∴AM=CN,
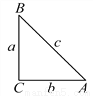
∴AB=AM+BM=CN+BM=4+6=10cm. 如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA=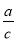 ,cosA=
,cosA=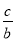 ,tanA=
,tanA=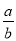 .我们不难发现:sin260°+cos260°=1,…,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…,试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
 sin2A+cos2A=1,tanA=,理由见解析.
【解析】试题分析:sin2A+cos2A=1,tanA=,根据三角函数的定义以及勾股定理通过推导即可得.
试题解析:sin2A+cos2A=1,tanA=,理由如下:
∵∠C=90°,∴a2+b2=c2,sinA=,cosA=,tanA=,
∴sin2A+cos2A=;
tanA=..
sin2A+cos2A=1,tanA=,理由见解析.
【解析】试题分析:sin2A+cos2A=1,tanA=,根据三角函数的定义以及勾股定理通过推导即可得.
试题解析:sin2A+cos2A=1,tanA=,理由如下:
∵∠C=90°,∴a2+b2=c2,sinA=,cosA=,tanA=,
∴sin2A+cos2A=;
tanA=.. 
