题目内容
如图,ΔABC≌ΔCDA,∠BAC=∠DCA,则BC的对应边是 ( )
A. CD B. CA C. DA D. AB
 C
【解析】∵ΔABC≌ΔCDA,∠BAC=∠DCA,
∴BC的对应边为DA,
故选C.
C
【解析】∵ΔABC≌ΔCDA,∠BAC=∠DCA,
∴BC的对应边为DA,
故选C.
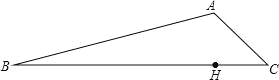
如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.
(1)求BC的长度;
(2)如果两个分队在前往A地时匀速前行,且甲的速度是乙的速度的三倍.试判断哪个分队先到达A地.(tan55°≈1.4,sin55°≈0.84,cos55°≈0.6,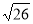 ≈5.01,结果保留整数)
≈5.01,结果保留整数)
 (1)、15360m;(2)、乙
【解析】
试题分析:(1)、利用坡度的定义得出AH的长,再利用tan∠HAC=,得出CH的长,进而得出答案;(2)、利用勾股定理得出AB的长利用cos∠HAC=,得出AC的长进而得出答案.
试题解析:(1)、连接AH ∵H在A的正南方向, ∴AH⊥BC, ∵AB的坡度为:1:5,
∴在Rt△ABH中, =, ∴AH=12000×=2400(...
(1)、15360m;(2)、乙
【解析】
试题分析:(1)、利用坡度的定义得出AH的长,再利用tan∠HAC=,得出CH的长,进而得出答案;(2)、利用勾股定理得出AB的长利用cos∠HAC=,得出AC的长进而得出答案.
试题解析:(1)、连接AH ∵H在A的正南方向, ∴AH⊥BC, ∵AB的坡度为:1:5,
∴在Rt△ABH中, =, ∴AH=12000×=2400(... 下面说法正确的是个数有( )
①如果三角形三个内角的比是1:2:3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;
③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;④如果∠A=∠B=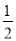 ∠C,那么△ABC是直角三角形;⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在△ABC中,若∠A+∠B=∠C,则此三角形是直角三角形.
∠C,那么△ABC是直角三角形;⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在△ABC中,若∠A+∠B=∠C,则此三角形是直角三角形.
A. 3个 B. 4个 C. 5个 D. 6个
 D
【解析】试题分析:对各个选项逐一进行计算并判断,即可得出答案.
【解析】
①根据三角形三个内角的比是1:2:3,求出这个三角形的最大内角度数是 ,故这个三角形是直角三角形,故正确;
②三角形的一个外角等于与它相邻的一个内角,而三角形的这个外角与它相邻的内角的和为,故三角形的这个外角与它相邻的内角分别为,故这个三角形是直角三角形,故正确;
③因为直角三角形的两条直角边互...
D
【解析】试题分析:对各个选项逐一进行计算并判断,即可得出答案.
【解析】
①根据三角形三个内角的比是1:2:3,求出这个三角形的最大内角度数是 ,故这个三角形是直角三角形,故正确;
②三角形的一个外角等于与它相邻的一个内角,而三角形的这个外角与它相邻的内角的和为,故三角形的这个外角与它相邻的内角分别为,故这个三角形是直角三角形,故正确;
③因为直角三角形的两条直角边互... 下图是小明在平面镜里看到的电子钟示数,这时的实际时间是________
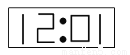
 15:01或10:51
【解析】∵没说明平面镜在电子钟的相对位置,
∴有两种可能,
当平面镜是在电子钟的下方,则原来的实际时间是15:01;
当平面镜是在电子钟的左侧,则原来的实际时间是10:51,
故答案为:15:01或10:51.
15:01或10:51
【解析】∵没说明平面镜在电子钟的相对位置,
∴有两种可能,
当平面镜是在电子钟的下方,则原来的实际时间是15:01;
当平面镜是在电子钟的左侧,则原来的实际时间是10:51,
故答案为:15:01或10:51. 公路BC所在的直线恰为AD的垂直平分线,则下列说法中:①小明从家到书店与小颖从家到书店一样远;②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;④小明从家到学校与小颖从家到学校一样远. 正确的是()
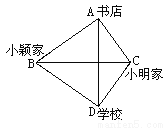
A. ①③ B. ②③ C. ②④ D. ③④
 B
【解析】∵公路BC所在的直线恰为AD的垂直平分线,
∴ΔABC≌ΔDBC,
∴CA=CB,BA=BD,
故可判断出②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;
而无法判断出①小明从家到书店与小颖从家到书店一样远;④小明从家到学校与小颖从家到学校一样远,
故选B.
B
【解析】∵公路BC所在的直线恰为AD的垂直平分线,
∴ΔABC≌ΔDBC,
∴CA=CB,BA=BD,
故可判断出②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;
而无法判断出①小明从家到书店与小颖从家到书店一样远;④小明从家到学校与小颖从家到学校一样远,
故选B. 下列说法正确的是( ).
A.所有正方形都是全等图形
B.面积相等的两个三角形是全等图形
C.所有半径相等的圆都是全等图形
D.所有长方形都是全等图形
 C.
【解析】
试题分析:根据全等图形的定义进行判断. A、所有正方形不一定是全等图形,故此选项错误;B、面积相等的两三角形不一定全等,故此选项错误;C、所有半径相等的圆都是全等图形,故此选项正确;D、所有长方形不一定是全等图形,故此选项错误.
故选:C.
C.
【解析】
试题分析:根据全等图形的定义进行判断. A、所有正方形不一定是全等图形,故此选项错误;B、面积相等的两三角形不一定全等,故此选项错误;C、所有半径相等的圆都是全等图形,故此选项正确;D、所有长方形不一定是全等图形,故此选项错误.
故选:C. 一个袋中装有2个红球,3个白球,和5个黄球,每个球除了顔色外都相同,从中任意摸出一个球,分别求出摸到红球,白球,黄球的概率。
 ,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即
,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即 已知粉笔盒里只有2支红色粉笔和3支白色粉笔,每支粉笔除颜色外其他均相同,现从中任取一支粉笔,则取出白色粉笔的概率是( )
A. 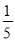 B.
B. 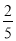 C.
C. 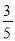 D.
D. 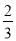
 C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C.
C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C. 如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 ________度.

 110
【解析】∵∠ABC=∠ADC=90°,CB=CD,且CA=CA,
∴△ABC≌△ADC,
∴∠BCA=∠DCA,
∵∠BAC=35°,∠ABC=90°,
∴∠BCA=55°,
∴∠BCD=2∠BCA=110°,
故答案为:110.
110
【解析】∵∠ABC=∠ADC=90°,CB=CD,且CA=CA,
∴△ABC≌△ADC,
∴∠BCA=∠DCA,
∵∠BAC=35°,∠ABC=90°,
∴∠BCA=55°,
∴∠BCD=2∠BCA=110°,
故答案为:110. 
