题目内容
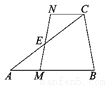
如图,E点为△ABC的边AC的中点,CN∥AB,过E点作直线交AB于M点,交CN于N点,若MB=6cm,CN=4cm,则AB=__cm.
 10
【解析】试题分析:由CN∥AB,可得∠NCE=∠MAE,再结合E是AC中点,对顶角相等,即可证得△CHE≌△MAE,从而得到结果.
∵CN∥AB,
∴∠NCE=∠MAE,
∵E是AC中点,
∴AE=CE,
∵∠AEM=∠CEN,
∴△CHE≌△MAE,
∴AM=CN,
∴AB=AM+BM=CN+BM=4+6=10cm.
10
【解析】试题分析:由CN∥AB,可得∠NCE=∠MAE,再结合E是AC中点,对顶角相等,即可证得△CHE≌△MAE,从而得到结果.
∵CN∥AB,
∴∠NCE=∠MAE,
∵E是AC中点,
∴AE=CE,
∵∠AEM=∠CEN,
∴△CHE≌△MAE,
∴AM=CN,
∴AB=AM+BM=CN+BM=4+6=10cm.
下面说法正确的是个数有( )
①如果三角形三个内角的比是1:2:3,那么这个三角形是直角三角形;
②如果三角形的一个外角等于与它相邻的一个内角,则这么三角形是直角三角形;
③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;④如果∠A=∠B=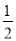 ∠C,那么△ABC是直角三角形;⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在△ABC中,若∠A+∠B=∠C,则此三角形是直角三角形.
∠C,那么△ABC是直角三角形;⑤若三角形的一个内角等于另两个内角之差,那么这个三角形是直角三角形;⑥在△ABC中,若∠A+∠B=∠C,则此三角形是直角三角形.
A. 3个 B. 4个 C. 5个 D. 6个
 D
【解析】试题分析:对各个选项逐一进行计算并判断,即可得出答案.
【解析】
①根据三角形三个内角的比是1:2:3,求出这个三角形的最大内角度数是 ,故这个三角形是直角三角形,故正确;
②三角形的一个外角等于与它相邻的一个内角,而三角形的这个外角与它相邻的内角的和为,故三角形的这个外角与它相邻的内角分别为,故这个三角形是直角三角形,故正确;
③因为直角三角形的两条直角边互...
D
【解析】试题分析:对各个选项逐一进行计算并判断,即可得出答案.
【解析】
①根据三角形三个内角的比是1:2:3,求出这个三角形的最大内角度数是 ,故这个三角形是直角三角形,故正确;
②三角形的一个外角等于与它相邻的一个内角,而三角形的这个外角与它相邻的内角的和为,故三角形的这个外角与它相邻的内角分别为,故这个三角形是直角三角形,故正确;
③因为直角三角形的两条直角边互... 一个袋中装有2个红球,3个白球,和5个黄球,每个球除了顔色外都相同,从中任意摸出一个球,分别求出摸到红球,白球,黄球的概率。
 ,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即
,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即 已知粉笔盒里只有2支红色粉笔和3支白色粉笔,每支粉笔除颜色外其他均相同,现从中任取一支粉笔,则取出白色粉笔的概率是( )
A. 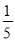 B.
B. 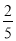 C.
C. 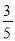 D.
D. 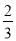
 C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C.
C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C. 已知△ABC.求作:△A′B′C′,使△A′B′C′≌△ABC.
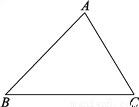
 作图见解析
【解析】试题分析:本题可利用全等三角形的判定定理SSS作图,作AC=A′C′,A′B′=AB,BC=B′C′;根据全等三角形的判定可得△A′B′C′≌△ABC,注意尺规作图中作一条线段等于已知线段的作法.
试题解析:作法:①任意作一条射线B′M,以点B′为圆心,以BC为半径画弧,交射线于点C′;
②分别以点B′和点C′为圆心,以AB和AC为半径画弧,交于点A′,连接A...
作图见解析
【解析】试题分析:本题可利用全等三角形的判定定理SSS作图,作AC=A′C′,A′B′=AB,BC=B′C′;根据全等三角形的判定可得△A′B′C′≌△ABC,注意尺规作图中作一条线段等于已知线段的作法.
试题解析:作法:①任意作一条射线B′M,以点B′为圆心,以BC为半径画弧,交射线于点C′;
②分别以点B′和点C′为圆心,以AB和AC为半径画弧,交于点A′,连接A... 如图,∠A=∠B,∠C=α,DE⊥AC,FD⊥AB,则∠EDF等于( )
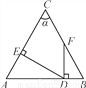
A. α B. 90°-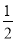 α C. 90°-α D. 180°-2α
α C. 90°-α D. 180°-2α
 B
【解析】∵∠A=∠B,∠C=α,
∴∠A=∠B=(180°-α),
∵DE⊥AC,FD⊥AB,
∴∠AED=∠FDB=90°,
∴∠ADE=90°-(180°-α)=α,
∴∠EDF =180°-90°-α=90°-α,
故选B.
B
【解析】∵∠A=∠B,∠C=α,
∴∠A=∠B=(180°-α),
∵DE⊥AC,FD⊥AB,
∴∠AED=∠FDB=90°,
∴∠ADE=90°-(180°-α)=α,
∴∠EDF =180°-90°-α=90°-α,
故选B. 如图,已知点P为∠MON内一点,点P与点A关于直线ON对称,点P与点B关于直线OM对称.连接AB,交ON于D点,交OM于C点,若AB长为15 cm,求△PCD的周长.
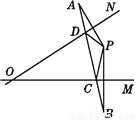
 15 cm.
【解析】由点P与点A关于直线ON对称,点P与点B关于直线OM对称可得:ON垂直平分AP,OM垂直平分BP;根据垂直平分线的性质可得DA=DP,CP=CB,通过等量代换得到△PCD的周长与AB的数量关系,即可求解.
【解析】
∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,
∴ON垂直平分AP,OM垂直平分BP,
∴DA=DP,CP=CB,
∴...
15 cm.
【解析】由点P与点A关于直线ON对称,点P与点B关于直线OM对称可得:ON垂直平分AP,OM垂直平分BP;根据垂直平分线的性质可得DA=DP,CP=CB,通过等量代换得到△PCD的周长与AB的数量关系,即可求解.
【解析】
∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,
∴ON垂直平分AP,OM垂直平分BP,
∴DA=DP,CP=CB,
∴... 如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 ________度.

 110
【解析】∵∠ABC=∠ADC=90°,CB=CD,且CA=CA,
∴△ABC≌△ADC,
∴∠BCA=∠DCA,
∵∠BAC=35°,∠ABC=90°,
∴∠BCA=55°,
∴∠BCD=2∠BCA=110°,
故答案为:110.
110
【解析】∵∠ABC=∠ADC=90°,CB=CD,且CA=CA,
∴△ABC≌△ADC,
∴∠BCA=∠DCA,
∵∠BAC=35°,∠ABC=90°,
∴∠BCA=55°,
∴∠BCD=2∠BCA=110°,
故答案为:110. 根据下列证明过程填空:
如图,已知BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C
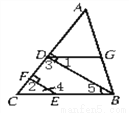
证明:∵BD⊥AC,EF⊥AC
∴∠2=∠3=90°( )
∴BD∥EF ( )
∴∠4=_____( )
∵∠1=∠4
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
 见解析
【解析】试题分析:解决问题要熟悉平行线的性质和判定,能正确运用语言叙述理由,还要注意平行线的性质和判定的综合运用.
试题解析:∵BD⊥AC,EF⊥AC(已知),
∴∠2=∠3=90°,
∴BD∥EF(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,同位角相等);
∵∠1=∠4(已知),
∴∠1=∠5(等量代换),
∴DG∥BC(内错角相...
见解析
【解析】试题分析:解决问题要熟悉平行线的性质和判定,能正确运用语言叙述理由,还要注意平行线的性质和判定的综合运用.
试题解析:∵BD⊥AC,EF⊥AC(已知),
∴∠2=∠3=90°,
∴BD∥EF(同位角相等,两直线平行),
∴∠4=∠5(两直线平行,同位角相等);
∵∠1=∠4(已知),
∴∠1=∠5(等量代换),
∴DG∥BC(内错角相... 
