题目内容
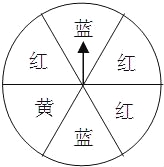
如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是( )
A.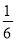 B.
B.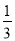 C.
C.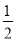 D.
D.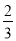
 A
【解析】
试题解析:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率=.
故选A.
A
【解析】
试题解析:∵转盘被等分成6个扇形区域,
而黄色区域占其中的一个,
∴指针指向黄色区域的概率=.
故选A.
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
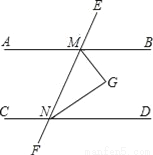
轻松课堂单元测试AB卷系列答案如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=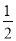 ∠BMN
∠BMN
同理∠GNM=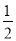 ∠DNM.
∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
 已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(...
已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(... 公路BC所在的直线恰为AD的垂直平分线,则下列说法中:①小明从家到书店与小颖从家到书店一样远;②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;④小明从家到学校与小颖从家到学校一样远. 正确的是()
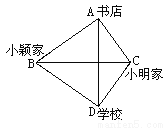
A. ①③ B. ②③ C. ②④ D. ③④
 B
【解析】∵公路BC所在的直线恰为AD的垂直平分线,
∴ΔABC≌ΔDBC,
∴CA=CB,BA=BD,
故可判断出②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;
而无法判断出①小明从家到书店与小颖从家到书店一样远;④小明从家到学校与小颖从家到学校一样远,
故选B.
B
【解析】∵公路BC所在的直线恰为AD的垂直平分线,
∴ΔABC≌ΔDBC,
∴CA=CB,BA=BD,
故可判断出②小明从家到书店与从家到学校一样远;③小颖从家到书店与从家到学校一样远;
而无法判断出①小明从家到书店与小颖从家到书店一样远;④小明从家到学校与小颖从家到学校一样远,
故选B. 一个袋中装有2个红球,3个白球,和5个黄球,每个球除了顔色外都相同,从中任意摸出一个球,分别求出摸到红球,白球,黄球的概率。
 ,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即
,,
【解析】
试题分析:先求出球的总个数,根据概率的定义直接计算即可.概率=所求情况数与总情况数之比.
试题解析:摸到红球的概率为即,摸到白球的概率为
摸到白球的概率为,即 从分别标有1、2、3、4的四张卡片中,一次同时抽2张,其中和为奇数的概率是 .
 【解析】试题分析:如图所示,
由树状图可知共有4×3=12种可能,和为奇数的有8种,所以概率是=.故答案为: .
【解析】试题分析:如图所示,
由树状图可知共有4×3=12种可能,和为奇数的有8种,所以概率是=.故答案为: . 已知粉笔盒里只有2支红色粉笔和3支白色粉笔,每支粉笔除颜色外其他均相同,现从中任取一支粉笔,则取出白色粉笔的概率是( )
A. 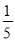 B.
B. 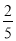 C.
C. 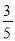 D.
D. 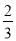
 C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C.
C
【解析】因为一共有5支粉笔,其中白粉笔有3支,取出白色粉笔的概率是,故选C. 已知△ABC.求作:△A′B′C′,使△A′B′C′≌△ABC.
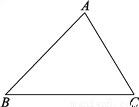
 作图见解析
【解析】试题分析:本题可利用全等三角形的判定定理SSS作图,作AC=A′C′,A′B′=AB,BC=B′C′;根据全等三角形的判定可得△A′B′C′≌△ABC,注意尺规作图中作一条线段等于已知线段的作法.
试题解析:作法:①任意作一条射线B′M,以点B′为圆心,以BC为半径画弧,交射线于点C′;
②分别以点B′和点C′为圆心,以AB和AC为半径画弧,交于点A′,连接A...
作图见解析
【解析】试题分析:本题可利用全等三角形的判定定理SSS作图,作AC=A′C′,A′B′=AB,BC=B′C′;根据全等三角形的判定可得△A′B′C′≌△ABC,注意尺规作图中作一条线段等于已知线段的作法.
试题解析:作法:①任意作一条射线B′M,以点B′为圆心,以BC为半径画弧,交射线于点C′;
②分别以点B′和点C′为圆心,以AB和AC为半径画弧,交于点A′,连接A... 如图,已知点P为∠MON内一点,点P与点A关于直线ON对称,点P与点B关于直线OM对称.连接AB,交ON于D点,交OM于C点,若AB长为15 cm,求△PCD的周长.
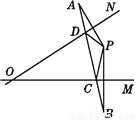
 15 cm.
【解析】由点P与点A关于直线ON对称,点P与点B关于直线OM对称可得:ON垂直平分AP,OM垂直平分BP;根据垂直平分线的性质可得DA=DP,CP=CB,通过等量代换得到△PCD的周长与AB的数量关系,即可求解.
【解析】
∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,
∴ON垂直平分AP,OM垂直平分BP,
∴DA=DP,CP=CB,
∴...
15 cm.
【解析】由点P与点A关于直线ON对称,点P与点B关于直线OM对称可得:ON垂直平分AP,OM垂直平分BP;根据垂直平分线的性质可得DA=DP,CP=CB,通过等量代换得到△PCD的周长与AB的数量关系,即可求解.
【解析】
∵点P与点A关于直线ON对称,点P与点B关于直线OM对称,
∴ON垂直平分AP,OM垂直平分BP,
∴DA=DP,CP=CB,
∴... 如图,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
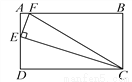
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
 (1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ...
(1)答案见解析;(2)
【解析】(1)根据矩形的性质可知∠A="∠D" =90°,再根据三角形的内角和为180°,可知∠DCE+∠DEC=900,由已知EF⊥EC,可得:∠AEF+∠DEC=900得出∠DCE=∠AEF,即可证明⊿AEF∽⊿DCE
(2)由(1)可知:⊿AEF∽⊿DCE ∴=
在矩形ABCD中,E为AD 的中点。
AB=2AD ∴ DC=AB=4AE ∴ ... 
