题目内容
20.在⊙O中,弦AB=4cm,O到AB的距离为1.5cm,则⊙O的半径为2.5cm.分析 根据题意画出图形,先根据垂径定理求出AD的长,连接OA,再由勾股定理即可得出结论.
解答  解:如图所示,
解:如图所示,
∵AB=4cm,OD⊥AB,
∴AD=$\frac{1}{2}$AB=2cm.
∵OD=1.5cm,
∴OA=$\sqrt{{OD}^{2}+{AD}^{2}}$=$\sqrt{{1.5}^{2}+{2}^{2}}$=2.5cm.
故答案为:2.5cm.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
10.化简$\frac{1}{a-1}$+$\frac{a}{1-a}$=( )
| A. | 0 | B. | 1 | C. | 1+a | D. | -1 |
5.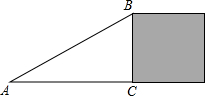 如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
 如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )
如图,△ABC为直角三角形,斜边AB长为20cm,阴影部分是正方形,其面积为144cm2,则AC边的长为( )| A. | 256cm | B. | 8cm | C. | 16cm | D. | 32cm |
 把抛物线y=x2先向左平移1个单位长度,再向下平移4个单位长度,得到如图所示的二次函数的图象.
把抛物线y=x2先向左平移1个单位长度,再向下平移4个单位长度,得到如图所示的二次函数的图象.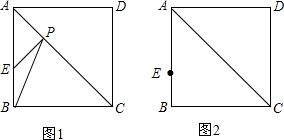 如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.
如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.