题目内容
8.已知以下三个二次方程有公共根ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0,①求这三个方程的根;
②求式子$\frac{{a}^{3}+{b}^{3}+{c}^{3}}{abc}$的值.
分析 ①把x=t代入3个方程得出a•t2+bt+c=0,bt2+ct+a=0,ct2+a•t+b=0,3个方程相加即可得出(a+b+c)(t2+t+1)=0,即可求出答案.
②a+b+c=0,即a+b=-c,接着把a3+b3用立方和公式分解,然后用-c代换a+b,原分式约分后把a2+b2配方,再用-c代换a+b,最后进行约分即可得到原分式的值.
解答 解:①设这三个方程的一个公共根为t.
把x=t代入ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0得:
a•t2+bt+c=0,bt2+ct+a=0,ct2+a•t+b=0,
相加得:(a+b+c)t2+(b+c+a)t+(a+b+c)=0,
(a+b+c)(t2+t+1)=0,
∵t2+t+1≠0,
∴a+b+c=0.
则t=1.故这三个方程的公共根为x=1.
②由a+b+c=0,得
a+b=-c,
原式=$\frac{(a+b)({a}^{2}-ab+{b}^{2})+{c}^{3}}{abc}$
=$\frac{-c({a}^{2}-ab+{b}^{2})+{c}^{3}}{abc}$
=$\frac{{c}^{2}-({a}^{2}-ab+{b}^{2})}{ab}$
=$\frac{{c}^{2}-[(a+b){\\;}^{2}-3ab]}{ab}$
=$\frac{{c}^{2}-{c}^{2}+3ab}{ab}$
=3.
点评 本题考查了一元二次方程的解:使一元二次方程左右两边成立的未知数的值叫一元二次的解.也考查了分式的化简求值.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
18.下列运算正确的是( )
| A. | 3x-x=3 | B. | x2•x3=x5 | C. | x6÷x2=x3 | D. | (x2)3=x5 |
3.随着我国人口增长速度的减慢,小学入学儿童数量有所减少,下表中数据近似地呈现了某地儿童入学年份的变化趋势:
则上表中的自变量是x(用字母表示)
| 年份x(年) | 2012 | 2013 | 2014 | … |
| 入学儿童人数y(人) | 2520 | 2330 | 2140 | … |
13.下列命题中是假命题的是( )
| A. | 多边形的外角和等于360° | |
| B. | 直角三角形的外角中可以有锐角 | |
| C. | 三角形两边之差小于第三边 | |
| D. | 如果两个角大小相等,且它们的和等于平角,那么这两个角都是直角 |
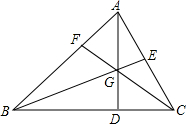 如图,在△ABC中,点D、E、F分别在三边上,点E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是30,△AGE的面积为3.
如图,在△ABC中,点D、E、F分别在三边上,点E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是30,△AGE的面积为3.