题目内容
12.F是正方形ABCD的对角线AC上一点,AF=AD,FG⊥AC于F,交CD于G,那么∠DFG=22.5°.分析 由正方形的性质得出∠DAF=$\frac{1}{2}$∠BAD=45°,由AF=AD,得出∠AFD=67.5°,再由∠AFG=90°,即可得出∠DFG的度数.
解答 解:如图所示:
∵四边形ABCD是正方形,
∴∠BAD=90°,∠DAF=$\frac{1}{2}$∠BAD=45°,
∵AF=AD,
∴∠AFD=$\frac{1}{2}$(180°-45°)=67.5°,
∵FG⊥AC,
∴∠AFG=90°,
∴∠DFG=90°-67.5°=22.5°;
故答案为:22.5°.
点评 本题考查了正方形的性质、等腰三角形的性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
3.随着我国人口增长速度的减慢,小学入学儿童数量有所减少,下表中数据近似地呈现了某地儿童入学年份的变化趋势:
则上表中的自变量是x(用字母表示)
| 年份x(年) | 2012 | 2013 | 2014 | … |
| 入学儿童人数y(人) | 2520 | 2330 | 2140 | … |
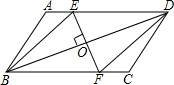 已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?
已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?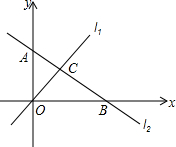 如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).
如图,直线l1:y=2x和直线l2:y=kx+b交于C点,A(0,2),B(4,0).