题目内容
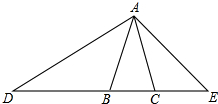
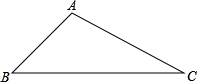 如图,在△ABC中,∠B=45°,∠C=15°,BC=5
如图,在△ABC中,∠B=45°,∠C=15°,BC=5| 2 |
考点:解直角三角形
专题:计算题
分析:作AH⊥BC于H,作∠DAC=15°,AD交BC于D,如图,易得∠ADH=30°,设AH=x,在Rt△AHD中,利用含30度的直角三角形三边的关系得到AD=2AH=2x,DH=
AH=
x,则DC=DA=2x,在Rt△ABH中利用∠B=45°得到BH=AH=x,所以3x+
x=5
,解得x=
,然后根据三角形面积公式求解.
| 3 |
| 3 |
| 3 |
| 2 |
15
| ||||
| 6 |
解答: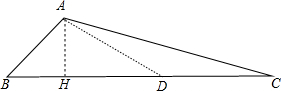 解:作AH⊥BC于H,作∠DAC=15°,AD交BC于D,如图,
解:作AH⊥BC于H,作∠DAC=15°,AD交BC于D,如图,
∵∠C=15°,
∴∠ADH=∠DAC+∠C=30°,
设AH=x,
在Rt△AHD中,AD=2AH=2x,DH=
AH=
x,
∵∠DAC=∠C=15°,
∴DC=DA=2x,
在Rt△ABH中,∵∠B=45°,
∴BH=AH=x,
∴BC=x+
x+2x=3x+
x,
∴3x+
x=5
,解得x=
,
∴S△ABC=
•5
•
=
.
 解:作AH⊥BC于H,作∠DAC=15°,AD交BC于D,如图,
解:作AH⊥BC于H,作∠DAC=15°,AD交BC于D,如图,∵∠C=15°,
∴∠ADH=∠DAC+∠C=30°,
设AH=x,
在Rt△AHD中,AD=2AH=2x,DH=
| 3 |
| 3 |
∵∠DAC=∠C=15°,
∴DC=DA=2x,
在Rt△ABH中,∵∠B=45°,
∴BH=AH=x,
∴BC=x+
| 3 |
| 3 |
∴3x+
| 3 |
| 2 |
15
| ||||
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
15
| ||||
| 6 |
75-25
| ||
| 6 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
△ABO的顶点坐标分别是A(-3,3)、B(3,3)、O(0,0),试将△ABO放大,使△ABO与△EFO的位似比为1:2,则点E和点F的坐标可能分别为( )
| A、(-6,6),(6,6) |
| B、(6,-6),(6,6) |
| C、(-6,6),(6,-6) |
| D、(6,6),(-6,-6) |
某市2013年全年商品房销售面积约2596000平方米,用科学记数法表示为( )平方米.
| A、0.2596×107 |
| B、2.596×106 |
| C、2.596×107 |
| D、25.96×105 |
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
 如图,已知等腰△ABC中,AB=AC=2,点D在边BC的反向延长线上,且DB=3,点E在边BC的延长线上,且∠EAC=∠D.
如图,已知等腰△ABC中,AB=AC=2,点D在边BC的反向延长线上,且DB=3,点E在边BC的延长线上,且∠EAC=∠D.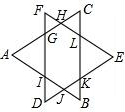 如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.