题目内容
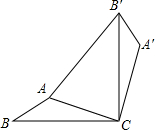 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( )
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( )| A、125° | B、130° |
| C、135° | D、140° |
考点:旋转的性质
专题:
分析:如图,作辅助线;首先证明∠AA′C=45°,然后证明AB′2=AA′2+A′B′2,得到∠AA′B′=90°,进而得到∠A′=135°,即可解决问题.
解答: 解:如图,连接AA′.由题意得:
解:如图,连接AA′.由题意得:
AC=A′C,A′B′=AB,∠ACA′=90°,
∴∠AA′C=45°,AA′2=22+22=8;
∵AB′2=32=9,A′B′2=12=1,
∴AB′2=AA′2+A′B′2,
∴∠AA′B′=90°,∠A′=135°,
故选C.
 解:如图,连接AA′.由题意得:
解:如图,连接AA′.由题意得:AC=A′C,A′B′=AB,∠ACA′=90°,
∴∠AA′C=45°,AA′2=22+22=8;
∵AB′2=32=9,A′B′2=12=1,
∴AB′2=AA′2+A′B′2,
∴∠AA′B′=90°,∠A′=135°,
故选C.
点评:该题主要考查了旋转变换的性质、勾股定理的逆定理及其应用问题;解题的关键是作辅助线,将分散的条件集中.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
某市2013年全年商品房销售面积约2596000平方米,用科学记数法表示为( )平方米.
| A、0.2596×107 |
| B、2.596×106 |
| C、2.596×107 |
| D、25.96×105 |
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
 如图,下面表述不正确的是( )
如图,下面表述不正确的是( )| A、∠1可表示为∠DAC |
| B、∠2可表示为∠BAC |
| C、∠BAD表示的角是∠1+∠2 |
| D、∠BAD可表示为∠A |
 已知如图,AE∥BF,问∠APB与∠PAE,∠PBF有怎样的关系?
已知如图,AE∥BF,问∠APB与∠PAE,∠PBF有怎样的关系? 如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
 (1)将半圆绕它的直径旋转一周形成的几何体是
(1)将半圆绕它的直径旋转一周形成的几何体是 已知AB为⊙O直径,CD平分∠ACB,AC=8,BC=6,则AD=
已知AB为⊙O直径,CD平分∠ACB,AC=8,BC=6,则AD=