题目内容
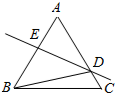 如图,等腰△ABC中,已知AB=AC,∠A=30°,AB的重直平分线交AC于D,交AB于E,求CBD的度数.
如图,等腰△ABC中,已知AB=AC,∠A=30°,AB的重直平分线交AC于D,交AB于E,求CBD的度数.考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:由等腰三角形的性质可求得∠ABC,由线段垂直平分线的性质可求得∠ABD=∠A=30°,可求得∠CBD的度数.
解答:解:
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=
=75°,
又D在AB的垂直平分线上,
∴DA=DB,
∴∠ABD=∠A=30°,
∴∠CBD=∠ABC-∠ABD=75°-30°=45°.
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=
| 180°-30° |
| 2 |
又D在AB的垂直平分线上,
∴DA=DB,
∴∠ABD=∠A=30°,
∴∠CBD=∠ABC-∠ABD=75°-30°=45°.
点评:本题主要考查线段垂直平分线的性质和等腰三角形的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
△ABO的顶点坐标分别是A(-3,3)、B(3,3)、O(0,0),试将△ABO放大,使△ABO与△EFO的位似比为1:2,则点E和点F的坐标可能分别为( )
| A、(-6,6),(6,6) |
| B、(6,-6),(6,6) |
| C、(-6,6),(6,-6) |
| D、(6,6),(-6,-6) |
某次抽奖活动在三个箱子中均有红、黄两种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖;摸出的三个球中只有两个红球的得二等奖;摸出的3个球只有1个红球的得三等奖;其余情况没有奖,则不中奖的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某市2013年全年商品房销售面积约2596000平方米,用科学记数法表示为( )平方米.
| A、0.2596×107 |
| B、2.596×106 |
| C、2.596×107 |
| D、25.96×105 |
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
 已知如图,AE∥BF,问∠APB与∠PAE,∠PBF有怎样的关系?
已知如图,AE∥BF,问∠APB与∠PAE,∠PBF有怎样的关系?