题目内容
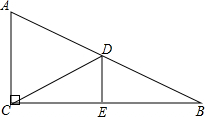 如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E.
如上图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC的垂直平分线交AB于点D,垂足为E.(1)求证:△ADC为等边三角形;
(2)若BD=2cm,BE=
| 3 |
考点:等边三角形的判定与性质,线段垂直平分线的性质,含30度角的直角三角形
专题:
分析:(1)先求出∠A=60°,再证出∠DCB=∠B=30°,得出∠ACD=60°,∠ADC=60°,得出∠ADC=∠A=∠ACD,因此△ADC为等边三角形;
(2)求出AC、BE、AB的长即可求出周长.
(2)求出AC、BE、AB的长即可求出周长.
解答:(1)证明:∵∠ACB=90°,∠B=30°,
∴∠A=60°,
∵DE是BC的垂直平分线,
∴CD=BD,
∴∠DCB=∠B=30°,
∴∠ACD=90°-30°=60°,∠ADC=∠B+∠DCB=60°,
∴∠ADC=∠A=∠ACD,
∴△ADC为等边三角形;
(2)解:由(1)得:△ADC是等边三角形,
∴AD=CD=AC,
∵DE是BC的垂直平分线,
∴CD=BD=2,CE=BE=
,
∴AC=CD=2,BC=2
,AB=4,
∴AB+AC+BC=4+2+2
=6+2
.
∴∠A=60°,
∵DE是BC的垂直平分线,
∴CD=BD,
∴∠DCB=∠B=30°,
∴∠ACD=90°-30°=60°,∠ADC=∠B+∠DCB=60°,
∴∠ADC=∠A=∠ACD,
∴△ADC为等边三角形;
(2)解:由(1)得:△ADC是等边三角形,
∴AD=CD=AC,
∵DE是BC的垂直平分线,
∴CD=BD=2,CE=BE=
| 3 |
∴AC=CD=2,BC=2
| 3 |
∴AB+AC+BC=4+2+2
| 3 |
| 3 |
点评:本题考查了等边三角形的判定与性质、线段垂直平分线的性质以及含30°角的直角三角形的性质;培养学生综合运用定理进行推理论证的能力.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
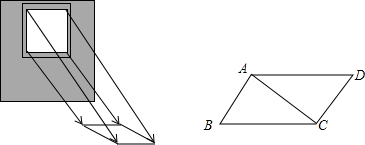
 在边长为a的菱形ABCD中,∠DAB=60°,E是AD上异于A,D两点的动点,F是CD上的动点,满足AE+CF=a
在边长为a的菱形ABCD中,∠DAB=60°,E是AD上异于A,D两点的动点,F是CD上的动点,满足AE+CF=a 已知AB为⊙O直径,CD平分∠ACB,AC=8,BC=6,则AD=
已知AB为⊙O直径,CD平分∠ACB,AC=8,BC=6,则AD=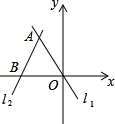 如图,已知:A(-1,2),S△AOB=
如图,已知:A(-1,2),S△AOB=
 如图,把△ABC的中线AD延长至E,使得DE=AD,连接EB,EC.求证:四边形ABEC是平行四边形.
如图,把△ABC的中线AD延长至E,使得DE=AD,连接EB,EC.求证:四边形ABEC是平行四边形.