题目内容
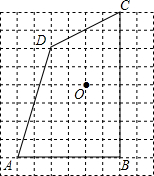 如图,在9×9网络图中,每个正方形边长均为1,点O和四边形ABCD的顶点均为小正方形的顶点.
如图,在9×9网络图中,每个正方形边长均为1,点O和四边形ABCD的顶点均为小正方形的顶点.(1)以O为位似中心,在网络中作四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD位似,且位似比为1:2.
(2)连接(1)中的A′O和D′O,则△A′OD′的面积为
考点:作图-位似变换
专题:
分析:(1)直接利用位似图形的性质得出对应点位置进而得出答案;
(2)利用网格可得出△A′OD′是直角三角形,再利用勾股定理以及三角形面积公式求出即可.
(2)利用网格可得出△A′OD′是直角三角形,再利用勾股定理以及三角形面积公式求出即可.
解答: 解:(1)如图所示:四边形A′B′C′D′即为所求;
解:(1)如图所示:四边形A′B′C′D′即为所求;
(2)
△A′OD′的面积为:
×OD′×OA′=
×
×2
=2.
故答案为:2.
 解:(1)如图所示:四边形A′B′C′D′即为所求;
解:(1)如图所示:四边形A′B′C′D′即为所求;(2)
△A′OD′的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:2.
点评:此题主要考查了勾股定理以及位似变换,得出对应点位置是解题关键.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,若∠C=30°,CD=2| 3 |
| A、π | ||||
| B、2π | ||||
C、
| ||||
D、
|
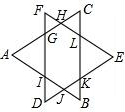 如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6.
如图,已知:边长相等的等边△ABC和等边△DEF重叠部分的周长是6. (1)将半圆绕它的直径旋转一周形成的几何体是
(1)将半圆绕它的直径旋转一周形成的几何体是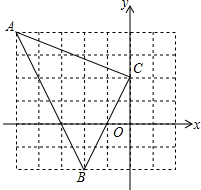 已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.
已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长. 已知AB为⊙O直径,CD平分∠ACB,AC=8,BC=6,则AD=
已知AB为⊙O直径,CD平分∠ACB,AC=8,BC=6,则AD= 如图所示,O是直线AB上一点,∠AOC:∠BOC=1:2,∠COD:∠AOC=1:2.
如图所示,O是直线AB上一点,∠AOC:∠BOC=1:2,∠COD:∠AOC=1:2.