题目内容
6.顺次连接等腰梯形各边中点所得的四边形的形状是( )| A. | 等腰梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
分析 顺次连接等腰梯形各边中点所得的四边形是菱形,理由为:根据题意画出相应的图形,连接AC、BD,由等腰梯形的性质得到AC=BD,由E、H分别为AD与DC的中点,得到EH为△ADC的中位线,利用三角形的中位线定理得到EH等于AC的一半,EH平行于AC,同理得到FG为△ABC的中位线,得到FG等于AC的一半,FG平行于AC,进而得到EH与FG平行且相等,利用一组对边平行且相等的四边形为平行四边形得到EFGH为平行四边形,再由EF为△ABD的中位线,得到EF等于BD的一半,进而由AC=BD得到EF=EH,根据一对邻边相等的平行四边形为菱形可得证.
解答 解:顺次连接等腰梯形各边中点所得的四边形是菱形,理由为:
已知:等腰梯形ABCD,E、F、G、H分别为AD、AB、BC、CD的中点,
求证:四边形EFGH为菱形.
证明:连接AC,BD,
∵四边形ABCD为等腰梯形,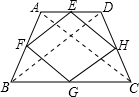
∴AC=BD,
∵E、H分别为AD、CD的中点,
∴EH为△ADC的中位线,
∴EH=$\frac{1}{2}$AC,EH∥AC,
同理FG=$\frac{1}{2}$AC,FG∥AC,
∴EH=FG,EH∥FG,
∴四边形EFGH为平行四边形,
同理EF为△ABD的中位线,
∴EF=$\frac{1}{2}$BD,又EH=$\frac{1}{2}$AC,且BD=AC,
∴EF=EH,
则四边形EFGH为菱形.
故选:D.
点评 此题考查了三角形的中位线定理,等腰梯形的性质,平行四边形的判定,以及菱形的判定,熟练掌握三角形中位线定理是解本题的关键.

练习册系列答案
相关题目
17.关于反比例函数y=$\frac{2}{x}$,下列说法正确的是( )
| A. | 函数图象位于二、四象限 | B. | 经过点(-4,0.5) | ||
| C. | y的值随x的增大而增大 | D. | 函数图象关于直线y=x轴对称 |
16. 一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )
一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )
 一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )
一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )| A. | x>2 | B. | x>0 | C. | x<2 | D. | x<0 |
 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°. 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数等于75°.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数等于75°.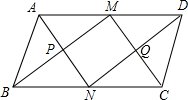 如图,M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,连接AN、DN、BM、CM,交点分别为P、Q.请判断四边形PMQN是什么特殊四边形?并证明你的结论.
如图,M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,连接AN、DN、BM、CM,交点分别为P、Q.请判断四边形PMQN是什么特殊四边形?并证明你的结论. 如图,在等腰梯形ABCD中,AD∥BC,过点A作AE∥CD,交BC于点E,若AB=2,AD=1.则四边形AECD的周长是6.
如图,在等腰梯形ABCD中,AD∥BC,过点A作AE∥CD,交BC于点E,若AB=2,AD=1.则四边形AECD的周长是6.