题目内容
18.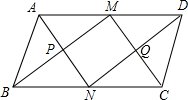 如图,M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,连接AN、DN、BM、CM,交点分别为P、Q.请判断四边形PMQN是什么特殊四边形?并证明你的结论.
如图,M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,连接AN、DN、BM、CM,交点分别为P、Q.请判断四边形PMQN是什么特殊四边形?并证明你的结论.
分析 首先证得四边形AMCN与四边形BNDM是平行四边形,继而可证得四边形PMQN为平行四边形,四边形ABNM是菱形,又由AN⊥BM,则可得四边形PMQN是矩形.
解答  解:四边形PMQN是矩形;
解:四边形PMQN是矩形;
证明:连接MN,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵M、N分别是AD、BC的中点,
∴AM∥CN,AM=CN,
∴四边形AMCN为平行四边形,
∴QM∥PN.
同理,四边形BNDM为平行四边形,
PM∥QN,
∴四边形PMQN为平行四边形,
∵AD∥BC,AD=BC,M、N是AD、BC中点,
∴AM∥BN,AM=BN=$\frac{1}{2}$AD,
∴四边形ABNM是平行四边形,
又∵AD=2AB,
∴AB=AM,
∴平行四边形ABNM是菱形,
∴AN⊥BM,
即∠MPN=90°,
∴平行四边形PMQN为矩形.
点评 本题综合考查了菱形及矩形的判定,应根据所要证明的结论进行合理推理,解题的关键是了解矩形的判定方法,难度中等.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
9.若点P(m,2)与点Q(5,n)关于原点对称,则m、n的值分别是( )
| A. | -5,2 | B. | 5,-2 | C. | 5,2 | D. | -5,-2 |
6.顺次连接等腰梯形各边中点所得的四边形的形状是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
13.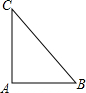 如图所示,A、B、C分别表示三个社区,BC=1500米.AB=900米,AC=1200米,在创建全国文明城市活动中,为了丰富人们生活,拟建一个文化活动中心,要求这三个社区到活动中心的距离相等,则活动中心M的位置应在( )
如图所示,A、B、C分别表示三个社区,BC=1500米.AB=900米,AC=1200米,在创建全国文明城市活动中,为了丰富人们生活,拟建一个文化活动中心,要求这三个社区到活动中心的距离相等,则活动中心M的位置应在( )
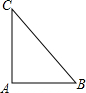 如图所示,A、B、C分别表示三个社区,BC=1500米.AB=900米,AC=1200米,在创建全国文明城市活动中,为了丰富人们生活,拟建一个文化活动中心,要求这三个社区到活动中心的距离相等,则活动中心M的位置应在( )
如图所示,A、B、C分别表示三个社区,BC=1500米.AB=900米,AC=1200米,在创建全国文明城市活动中,为了丰富人们生活,拟建一个文化活动中心,要求这三个社区到活动中心的距离相等,则活动中心M的位置应在( )| A. | AC的中点 | B. | BC的中点 | ||
| C. | AB的中点 | D. | ∠A的平分线与BC的交点 |
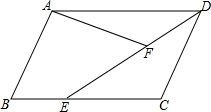 如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.
如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.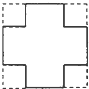 将边长为12cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形,如图所示,剩余部分折成一个无盖的长方体盒子,该盒子的容积是108cm3.
将边长为12cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形,如图所示,剩余部分折成一个无盖的长方体盒子,该盒子的容积是108cm3. 张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm.
张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm. 如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长(5$\sqrt{3}$-5)米.
如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长(5$\sqrt{3}$-5)米.