题目内容
15. 如图,在等腰梯形ABCD中,AD∥BC,过点A作AE∥CD,交BC于点E,若AB=2,AD=1.则四边形AECD的周长是6.
如图,在等腰梯形ABCD中,AD∥BC,过点A作AE∥CD,交BC于点E,若AB=2,AD=1.则四边形AECD的周长是6.
分析 先根据AD∥BC,AE∥CD得出四边形AECD是平行四边形,故AD=CE,AE=CD,再由AB=CD可得出AE=CD=AB,由此可得出结论.
解答 解:∵AD∥BC,AE∥CD,
∴四边形AECD是平行四边形,
∴AD=CE,AE=CD.
∵AB=CD=2,
∴AE=CD=AB=2,
∴四边形AECD的周长=2AD+2CD=2×1+2×2=6.
故答案为:6.
点评 本题考查的是等腰梯形的性质,熟知等腰梯形的两腰相等是解答此题的关键.

练习册系列答案
相关题目
6.顺次连接等腰梯形各边中点所得的四边形的形状是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
20. 小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )
小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )
 小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )
小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )| A. | 22° | B. | 22.5° | C. | 23° | D. | 25° |
5.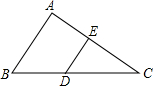 如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
 如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
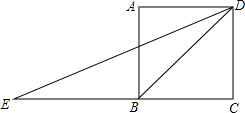 如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?
如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?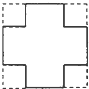 将边长为12cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形,如图所示,剩余部分折成一个无盖的长方体盒子,该盒子的容积是108cm3.
将边长为12cm的正方形铁片的四个角各剪去一个边长为3cm的小正方形,如图所示,剩余部分折成一个无盖的长方体盒子,该盒子的容积是108cm3. 张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm.
张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm.