题目内容
16. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
分析 连接CF,则∠D+∠E=∠1+∠2,则图中所求的几个角的和是五边形ABCFG的内角和.
解答  解:连接CF.
解:连接CF.
则∠1+∠2=∠D+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠BCD+∠1+∠2+∠EFG+∠G=(5-2)×180°=540°.
故∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是540°.
故答案为:540°.
点评 考查了多边形内角与外角,三角形内角和定理,根据三角形的内角和定理把求角的和的问题转化为求多边形的内角和的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.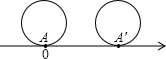 把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
 把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )
把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与原点重合,圆沿着数轴的方向滚动一周,点A的终点表示的数是( )| A. | π | B. | 2π | C. | 3.14 | D. | 6.28 |
1.已知直角三角形的三边a,b,c,且周长为15,斜边c=7,则△ABC的面积为( )
| A. | $\frac{15}{2}$ | B. | $\frac{15}{4}$ | C. | 15 | D. | $\frac{10}{4}$ |
6.顺次连接等腰梯形各边中点所得的四边形的形状是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
 如图,OE平分∠MON,∠FEO=28°,∠MFE=56°,试说明FE∥ON.
如图,OE平分∠MON,∠FEO=28°,∠MFE=56°,试说明FE∥ON.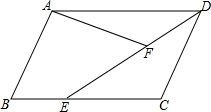 如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.
如图,在平行四边形ABCD中,已知E是BC上异于B、C的一点,∠AFE=∠B,AD=10,DC=6,AF=3,求DE.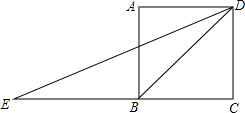 如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?
如图,正方形ABCD的边长为1,延长边CB到点E,使BE=BD.连接DE,∠CDE的度数是多少?