题目内容
11. 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数等于75°.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数等于75°.
分析 由矩形ABCD,得到OA=OB,根据AE平分∠BAD,得到等边三角形OAB,推出AB=OB,求出∠OAB、∠OBC的度数,根据平行线的性质和等角对等边得到OB=BE,根据三角形的内角和定理即可求出答案.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,
∴OA=OB,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°=∠AEB,
∴AB=BE,
∵∠CAE=15°,
∴∠DAC=45°-15°=30°,
∠BAC=60°,
∴△BAO是等边三角形,
∴AB=OB,∠ABO=60°,
∴∠OBC=90°-60°=30°,
∵AB=OB=BE,
∴∠BOE=∠BEO=$\frac{1}{2}$(180°-30°)=75°.
故答案为75°.
点评 本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是求出∠OBC的度数和求OB=BE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知直角三角形的三边a,b,c,且周长为15,斜边c=7,则△ABC的面积为( )
| A. | $\frac{15}{2}$ | B. | $\frac{15}{4}$ | C. | 15 | D. | $\frac{10}{4}$ |
6.顺次连接等腰梯形各边中点所得的四边形的形状是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
20. 小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )
小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )
 小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )
小明将等腰直角三角板放在两条平行线上,如图所示.若∠2=22°,则∠1的度数为( )| A. | 22° | B. | 22.5° | C. | 23° | D. | 25° |
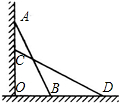 如图,一架云梯AB长25m,斜靠在一竖直的墙AO上,这时梯子底端B离墙的距离BO是7m,如果梯子的顶端A沿墙下滑了4m,那么梯子底部在水平方向也滑动了4m吗?请给以说明.
如图,一架云梯AB长25m,斜靠在一竖直的墙AO上,这时梯子底端B离墙的距离BO是7m,如果梯子的顶端A沿墙下滑了4m,那么梯子底部在水平方向也滑动了4m吗?请给以说明.