题目内容
7.$\sqrt{x-\sqrt{3}}$+(y-$\frac{1}{\sqrt{3}}$)2=0,则xy=1.分析 根据非负数的性质,即可解答.
解答 解:∵$\sqrt{x-\sqrt{3}}$+(y-$\frac{1}{\sqrt{3}}$)2=0,
∴$\left\{\begin{array}{l}{x-\sqrt{3}=0}\\{y-\frac{1}{\sqrt{3}}=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=\frac{1}{\sqrt{3}}}\end{array}\right.$,
∴xy=$\sqrt{3}×\frac{1}{\sqrt{3}}=1$.
故答案为:1.
点评 本题考查了非负数的性质,解决本题的关键是熟记非负数的性质.

练习册系列答案
相关题目
18.若x>y,则下列式子中错误的是( )
| A. | x-2>y-2 | B. | x+2>y+2 | C. | -2x>-2y | D. | $\frac{x}{2}$>$\frac{y}{2}$ |
15.已知点(1-2a,a-4)在第三象限,则整数a的值可以取( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
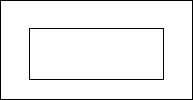 在一块长比宽多6米的矩形场地中央建造商店,它的周围都留3米宽的路,若使道路的面积与商店面积相等,求商店的长与宽各是多少米?
在一块长比宽多6米的矩形场地中央建造商店,它的周围都留3米宽的路,若使道路的面积与商店面积相等,求商店的长与宽各是多少米?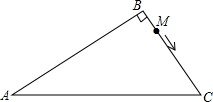 如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?
如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?