题目内容
17.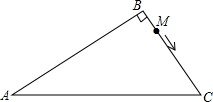 如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?
如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?
分析 利用M点运动的路线,分别利用当BM=$\frac{1}{4}$BC时以及当AM=$\frac{1}{4}$AC时求出即可.
解答 解:由题意可得:当BM=$\frac{1}{4}$BC时,△ABC的面积是△ABM面积的4倍,
∵∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,
∴BC=2cm,
故BM=$\frac{1}{4}$×2=$\frac{1}{2}$(cm)时,△ABC的面积是△ABM面积的4倍,
即点M出发$\frac{\frac{1}{2}}{\sqrt{2}}$=$\frac{\sqrt{2}}{4}$秒时,△ABC的面积是△ABM面积的4倍,
当AM=$\frac{1}{4}$AC时,△ABC的面积是△ABM面积的4倍,
故AM=$\frac{1}{4}$×4=1(cm)时,△ABC的面积是△ABM面积的4倍,
即点M出发$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$秒时,△ABC的面积是△ABM面积的4倍.
点评 此题主要考查了勾股定理,正确利用M点运动的轨迹得出BM与BC以及AM与AC的关系得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
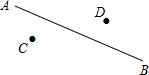 如图,在直线AB上找一点P,使PC=PD.(不写作法,但保留作图痕迹)
如图,在直线AB上找一点P,使PC=PD.(不写作法,但保留作图痕迹)