题目内容
14.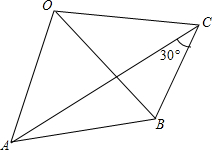 如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°.
如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°.
分析 由OA=OB=OC,得到以O为圆心,OA为半径的圆经过A,B,C,如图所示,利用同弧所对的圆心角等于所对圆周角的2倍即可求出∠AOB的度数.
解答  解:由OA=OB=OC,得到以O为圆心,OA长为半径的圆经过A,B及C,
解:由OA=OB=OC,得到以O为圆心,OA长为半径的圆经过A,B及C,
∵圆周角∠ACB与圆心角∠AOB都对$\widehat{AB}$,且∠ACB=30°,
∴∠AOB=2∠ACB=60°.
故答案为:60°.
点评 此题考查了圆周角定理,根据题意作出相应的圆O是解本题的关键.

练习册系列答案
相关题目
2.已知△ABC的三边长分别为a,b,c且a+b=4,ab=1,c=$\sqrt{14}$,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不能确定 |
9.三边均为整数,且最大边长为11的三角形共有( )个.
| A. | 20 | B. | 26 | C. | 30 | D. | 36 |
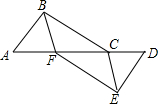 已知:如图,△FAB≌△CDE,BC=EF.求证:∠ACB=∠DFE.
已知:如图,△FAB≌△CDE,BC=EF.求证:∠ACB=∠DFE.
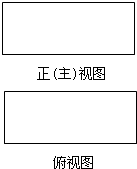 如图是长和宽分别相等的两个矩形.给定下列四个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图;④存在正方体,其正(主)视图、俯视图如图.其中真命题的个数是( )
如图是长和宽分别相等的两个矩形.给定下列四个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图;④存在正方体,其正(主)视图、俯视图如图.其中真命题的个数是( )