题目内容
4.阅读:△ABC中,a,b,c分别是∠A,∠B,∠C的对边,△ABC的边角有如下性质:①正弦定理:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$
②余弦定理:a2=b2+c2-2bccosA,b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
③S△ABC=$\frac{1}{2}$absin C=$\frac{1}{2}$bcsin A=$\frac{1}{2}$acsin B
请你根据上述结论求解下列问题:在锐角△ABC中,a,b,c分别是∠A,∠B,∠C的对边,且2asin B=$\sqrt{3}$b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积.
分析 (1)由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:asinB=bsinA,代入2asinB=$\sqrt{3}$b,可得sinA的值,即可求出角A的大小;
(2)由余弦定理得可得bc的值,再运用S△ABC=$\frac{1}{2}$bcsinA即可求出△ABC的面积.
解答 解:(1)∵2asinB=$\sqrt{3}$b,利用正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:asinB=bsinA,
∴2bsinA=$\sqrt{3}$b,
∵sinB≠0,
∴sinA=$\frac{\sqrt{3}}{2}$,
又∵A为锐角,
∴A=$\frac{π}{3}$;
(2)由余弦定理得:a2=b2+c2-2bc•cosA,即36=b2+c2-bc=(b+c)2-3bc=64-3bc,
∴bc=$\frac{28}{3}$,
又∵sinA=$\frac{\sqrt{3}}{2}$,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{7\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理与余弦定理,解题的关键是灵活运用正弦定理与余弦定理.

练习册系列答案
相关题目
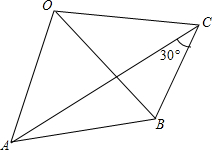 如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°.
如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°. 如图,∠1+∠2+∠3=232°,AB∥DF,BC∥DE,则∠3-∠1的度数为76°.
如图,∠1+∠2+∠3=232°,AB∥DF,BC∥DE,则∠3-∠1的度数为76°.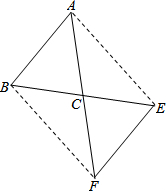 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.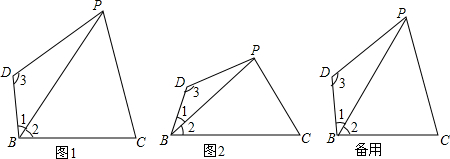
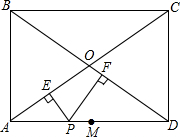 矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.
矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.