题目内容
3．
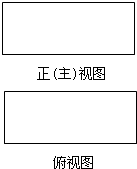如图是长和宽分别相等的两个矩形．给定下列四个命题：①存在三棱柱，其正（主）视图、俯视图如右图；②存在四棱柱，其正（主）视图、俯视图如右图；③存在圆柱，其正（主）视图、俯视图如右图；④存在正方体，其正（主）视图、俯视图如图．其中真命题的个数是（ ）| A． | 3 | B． | 2 | C． | 1 | D． | 4 |
分析 由俯视图可判断此几何体不可能为三棱柱和圆柱，由矩形的长宽不等，可判断此几何体不可能为正方体，而四棱柱的正（主）视图、俯视图都为矩形，于是可判断此几何体可能为四棱柱．
解答 解：由于正（主）视图、俯视图都为矩形，所以此几何体不可能为三棱柱和圆柱，由于每个矩形的长宽不等，所以此几何体不可能为正方体，此几何体可能为四棱柱．
故选C．
点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．也考查了三视图．
练习册系列答案
相关题目
17．下列计算中，正确的是（ ）
| A． | $\sqrt{（-9）×（-25）}$=$\sqrt{-9}×\sqrt{-25}$=（-3）×（-5）=15 | B． | -3$\sqrt{\frac{2}{3}}$=$\sqrt{（-3）^{2}×\frac{2}{3}}$=$\sqrt{6}$ | ||
| C． | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{（13+12）（13-12）}$=$\sqrt{25}$=5 | D． | 3$\sqrt{2}•4\sqrt{2}=12\sqrt{2}$ |
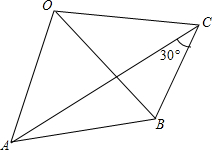如图，OA=OB=OC且∠ACB=30°，则∠AOB的大小是60°．
如图，∠1+∠2+∠3=232°，AB∥DF，BC∥DE，则∠3-∠1的度数为76°．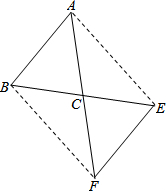
如图，在△ABC中，AB=AC，若将△ABC绕点C顺时针旋转180°得到△FEC．