题目内容
6.一个不透明的袋子中有除颜色外其余都相同的红、黄、蓝色玻璃球若干个,其中红色玻璃球有6个,黄色玻璃球有9个,已知从袋子中随机摸出一个蓝色玻璃球的概率为$\frac{2}{5}$,那么,随机摸出一个为红色玻璃球的概率为$\frac{6}{25}$.分析 首先设口袋中蓝色玻璃球有x个,根据概率公式,可得$\frac{x}{6+9+x}=\frac{2}{5}$,据此求出口袋中蓝色玻璃球的数量是多少;然后用口袋中红色玻璃球的数量除以玻璃球的总量,求出随机摸出一个为红色玻璃球的概率为多少即可.
解答 解:设口袋中蓝色玻璃球有x个,
则$\frac{x}{6+9+x}=\frac{2}{5}$,
解得x=10,
∴随机摸出一个为红色玻璃球的概率为:
6÷(6+9+10)
=6÷25
=$\frac{6}{25}$
∴随机摸出一个为红色玻璃球的概率为$\frac{6}{25}$.
故答案为:$\frac{6}{25}$.
点评 此题主要考查了概率公式的应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
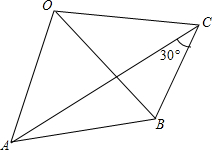 如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°.
如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°. 如图,∠1+∠2+∠3=232°,AB∥DF,BC∥DE,则∠3-∠1的度数为76°.
如图,∠1+∠2+∠3=232°,AB∥DF,BC∥DE,则∠3-∠1的度数为76°.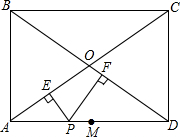 矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.
矩形ABCD中,PE⊥AC,PF⊥BD,点M是线段AD中点,求证:ME=MF.