题目内容
5．输入x，按如图所示程序进行运算：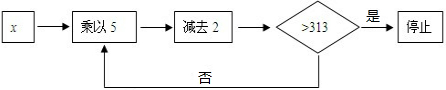
规定：程序运行到“判断大于313”记为一次运算．若输入x后程序运算3次停止，则x的取值范围为3＜x≤13．
分析 根据题意得出第一次输出的数为5x-2，第二次输出的数为5（5x-2）-2=25x-12，第三次输出的数为5[5（5x-2）-2]-2=125x-62，根据题意得出不等式组，求出不等式组的解集即可．
解答 解：第一次输出的数为5x-2，第二次输出的数为5（5x-2）-2=25x-12，
第三次输出的数为5[5（5x-2）-2]-2=125x-62，
由题意得：$\left\{\begin{array}{l}{25x-12≤313}\\{125x-62＞313}\end{array}\right.$，
解得：3＜x≤13
故答案为：3＜x≤13．
点评 本题考查了解一元一次不等式组的应用，解此题的关键是能得出关于x的不等式组，题目比较典型．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
17．下列计算中，正确的是（ ）
| A． | $\sqrt{（-9）×（-25）}$=$\sqrt{-9}×\sqrt{-25}$=（-3）×（-5）=15 | B． | -3$\sqrt{\frac{2}{3}}$=$\sqrt{（-3）^{2}×\frac{2}{3}}$=$\sqrt{6}$ | ||
| C． | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{（13+12）（13-12）}$=$\sqrt{25}$=5 | D． | 3$\sqrt{2}•4\sqrt{2}=12\sqrt{2}$ |
10．缸内红茶菌的面积每天长大一倍，若17天长满整个缸面，那么经过多少天长满缸面的一半（ ）
| A． | 8 | B． | 9 | C． | 15 | D． | 16 |
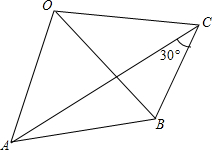如图，OA=OB=OC且∠ACB=30°，则∠AOB的大小是60°．
如图，∠1+∠2+∠3=232°，AB∥DF，BC∥DE，则∠3-∠1的度数为76°．