题目内容
9.三边均为整数,且最大边长为11的三角形共有( )个.| A. | 20 | B. | 26 | C. | 30 | D. | 36 |
分析 最长的边长度是11,另外两边长用x,y表示,要构成三角形必须x+y≥12,列举出当y分别从11,10,9,8,7,6时,对应的三角形的个数,根据分类计数原理得到结果.
解答 解:设另外两边长为x,y,且不妨设1≤x≤y≤11,要构成三角形,必须x+y≥12.
当y取值11时,x=1,2,3,…,11,可有11个三角形;
当y取值10时,x=2,3,…,10,可有9个三角形;
当y取值分别为9,8,7,6时,x取值个数分别是7,5,3,1,
∴根据分类计数原理知所求三角形的个数为11+9+7+5+3+1=36.
故选D.
点评 本题考查分类计数原理,以及三角形的三边关系,关键是掌握三角形的三边关系定理,注意分类讨论思想的应用.

练习册系列答案
相关题目
4.设P是高为h的正三角形内的一点,P到三边的距离分别为x,y,z(x≤y≤z).若以x,y,z为边可以组成三角形,则z应满足的条件为( )
| A. | $\frac{1}{4}$h≤z$<\frac{1}{3}$h | B. | $\frac{1}{3}$h≤z$<\frac{1}{2}$h | C. | $\frac{1}{2}$h≤z$<\frac{3}{4}$h | D. | $\frac{3}{4}h≤z<h$ |
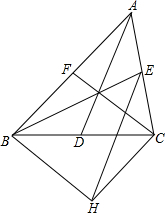 如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.
如图,△ABC的三条中线分别为AD、BE、CF,点H为△ABC外一点,且四边形BHCF为平行四边形,连接EH,试探究AD与EH的位置关系.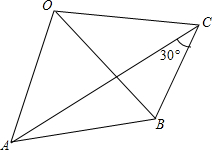 如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°.
如图,OA=OB=OC且∠ACB=30°,则∠AOB的大小是60°.