题目内容
10．（1）解方程：x2+4x-5=0；（2）解不等式组$\left\{\begin{array}{l}{2x-1≥5}\\{8-4x＜0}\end{array}\right.$．
分析 （1）利用因式分解法求解即可；
（2）先解不等式组中的每一个不等式，再求其公共解集即可．
解答 解：（1）原方程变形为（x-1）（x+5）=0，
所以x1=-5，x2=1；
（2）$\left\{\begin{array}{l}{2x-1≥5①}\\{8-4x＜0②}\end{array}\right.$，
由①得：x≥3，
由②得：x＞2，
所以不等式组的解集为：x≥3．
点评 本题考查了因式分解法解一元二次方程，当把方程通过移项把等式的右边化为0后方程的左边能因式分解时，一般情况下是把左边的式子因式分解，再利用积为0的特点解出方程的根．因式分解法是解一元二次方程的一种简便方法，要会灵活运用．也考查了解一元一次不等式组．
练习册系列答案
相关题目
如图，已知一次函数y=x-2与反比例函数y=$\frac{3}{x}$的图象交于A、B两点．
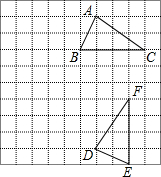如图，在小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，根据图形解答下列问题：
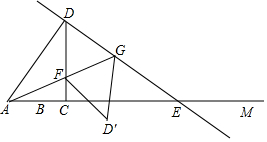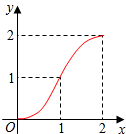
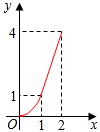
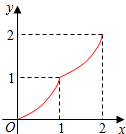
如图，射线AM上有一点B，AB=6，点C是射线AM上异于B的一点，过C作CD⊥AM，且CD=$\frac{4}{3}$AC，过D点作DE⊥AD，交射线AM于E，在射线CD取点F，使得CF=CB，连接AF并延长，交DE于点G，设AC=3x．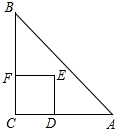
如图，Rt△ABC中，∠C=90°，AC=BC=2，正方形CDEF的顶点D、F分别在AC、BC上，C、D两点不重合，设CD的长度为x，Rt△ABC与正方形CDEF重叠部分的面积为y，则下列中能表示y与x之间的关系的是（ ）
