题目内容
18.已知二次函数y=x2-(2k+1)x+k2+k(k>0)(1)当k=$\frac{1}{2}$时,将这个二次函数的解析式写成顶点式;
(2)求证:关于x的一元二次方程x2-(2k+1)x+k2+k=0有两个不相等的实数根.
分析 (1)把k代入抛物线解析式,然后利用配方法可确定抛物线的顶点坐标;
(2)计算判别式的值,然后判别式的意义进行证明.
解答 (1)解:把k=$\frac{1}{2}$代入y=x2-(2k+1)x+k2+k(k>0)得y=x2-2x+$\frac{3}{4}$,
因为y=(x-1)2-$\frac{1}{4}$
所以抛物线的顶点坐标为(1,-$\frac{1}{4}$);
(2)证明:△=(2k+1)2-4(k2+k)=1>0,
所以关于x的一元二次方程x2-(2k+1)x+k2+k=0有两个不相等的实数根.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
 如图所示,某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系由下面的图象OBCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,则从甲地到乙地,这辆摩托车耗油量为0.9升,车修好后,摩托车的速度为30千米/小时.
如图所示,某人从甲地出发,骑摩托车去乙地,途中因车出现故障而停车修理,到达乙地时正好用了2小时,已知摩托车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系由下面的图象OBCD给出,若这辆摩托车平均每行驶100千米的耗油量为2升,则从甲地到乙地,这辆摩托车耗油量为0.9升,车修好后,摩托车的速度为30千米/小时. 如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,-1).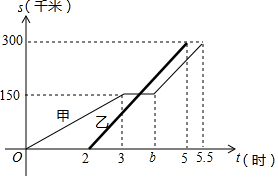 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.