题目内容
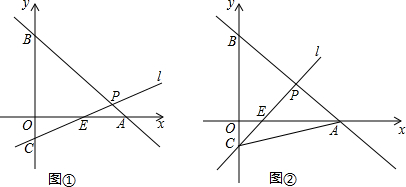
2.已知A(8,0),B(0,6),C(0,-2),连接AB,过点C的直线与AB交于点P,与x轴交于点E.(1)如图①,当PB=PC时,求点E和点P的坐标;
(2)如图②,若过点C的直线与x轴交于点E,且$\frac{OC}{OE}$=$\frac{5}{4}$,求点E和△PAC的面积.
分析 (1)过点P作PD⊥y轴于D,根据等腰三角形三线合一的性质求得BD=DC=4O,进而求得OD=OC=2,然后根据平行线分线段成比例定理即可求得PD,即可求得P的坐标,然后根据$\frac{OE}{PD}$=$\frac{OC}{CD}$,求得OE的长度,从而求得E的坐标.
(2)先求出E点的坐标,就可以求出直线AB、PC的解析式.求出两条直线的交点P,再根据S△PAC=S△PAE+S△CAE就可以求解.
解答 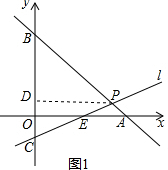 解:(1)如图1,过点P作PD⊥y轴于D,
解:(1)如图1,过点P作PD⊥y轴于D,
∵B(0,6),C(0,-2),
∴BC=8,
∵PB=PC,
∴BD=DC=4.
∵OB=6,
∴OD=2,OC=2,
∵PD∥OA,
∴$\frac{PD}{OA}$=$\frac{BD}{OB}$
即$\frac{PD}{8}$=$\frac{4}{6}$,
∴PD=$\frac{16}{3}$,
∴P($\frac{16}{3}$,2),
∵PD∥OA,
∴$\frac{OE}{PD}$=$\frac{OC}{CD}$,
即$\frac{OE}{\frac{16}{3}}$=$\frac{2}{4}$,
∴OE=$\frac{8}{3}$,
∴E($\frac{8}{3}$,0);
(2)如图2,∵$\frac{OC}{OE}$=$\frac{5}{4}$,OC=2,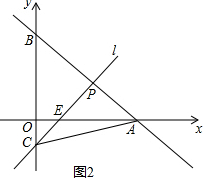
∴OE=$\frac{8}{5}$,
∴E($\frac{8}{5}$,0),
∴OE=8-$\frac{8}{5}$=$\frac{32}{5}$,
由题意可设直线PC的解析式为y=kx-2,
∵直线l经过E($\frac{8}{5}$,0),
∴$\frac{8}{5}$k-2=0,
∴k=$\frac{5}{4}$.
∴直线l的解析式为y=$\frac{5}{4}$x-2.
∵A(8,0),B(0,6),
∴直线AB的解析式为y=-$\frac{3}{4}$x+6.
解$\left\{\begin{array}{l}{y=-\frac{3}{4}x+6}\\{y=\frac{5}{4}x-2}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$.
∴P(4,3).
S△PAC=S△PAE+S△CAE=$\frac{1}{2}$×$\frac{32}{5}$×3+$\frac{1}{2}$×$\frac{32}{5}$×2=16.
点评 本题主要考查了平行线分线段成比例定理,待定系数法求函数解析式,并且考查不规则图形的面积可以转化为求一些规则图形或易求面积的图形的和或差的计算.

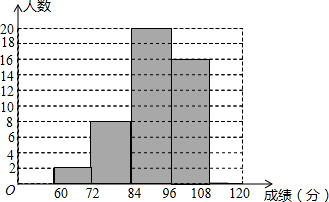 朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题.
朝宗实验学校初三年级的同学参加了吉州市的模拟统考,该校数学教师对本班数学成绩(成绩取整数,满分为120分)作了统计分析,绘制成频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题. | 频数 | 频率 | |
| 60<x≤72 | 2 | 0.04 |
| 72<x≤84 | 8 | 0.16 |
| 84<x≤96 | 20 | a |
| 96<x≤108 | 16 | 0.32 |
| 108<x≤120 | b | 0.08 |
| 合计 | 50 | 1 |
(2)补全频数分布直方图;
(3)为了激励学生,教师准备从超过108分的学生中选2人介绍学习经验,那么取得118分的小红和112分的小明同时被选上的概率是多少?请用列表法或画树形图加以说明,并列出所有可能的结果.
| A. | (-2,-3) | B. | (-1,-3) | C. | (-3,1) | D. | (-2,3) |
| A. | 4 | B. | -2 | C. | -4 | D. | 4或-4 |
| 日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 |
| 电表显示(度) | 117 | 120 | 124 | 129 | 135 | 138 | 142 | 145 |
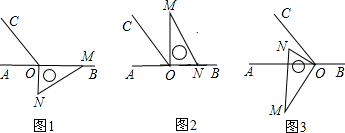
 如图,△ABC中,2∠BAC=∠ABC,2BC=AB,求证:AC⊥BC.
如图,△ABC中,2∠BAC=∠ABC,2BC=AB,求证:AC⊥BC.