题目内容
16.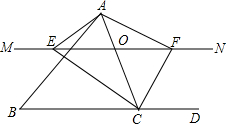 如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,点O是AC边上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)说明EO=FO;
(2)当点O运动到OA=$\frac{1}{2}$AC时,四边形AECF是矩形?说明你的结论.
(3)在(2)的条件下,当∠ACB=90°时,四边形AECF是正方形.
分析 (1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD及等角对等边即可证得OE=OF;
(2)根据矩形的性质可知:对角线互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.
(3)当∠ACB=90°时,四边形AECF是正方形;根据平行线的性质可得∠AOE=∠ACB=90°,进而可得AC⊥EF,再根据对角线互相垂直的矩形是正方形可得结论.
解答 (1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)解:当O运动到AO=$\frac{1}{2}$AC时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=$\frac{1}{2}$∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.
故答案为:$\frac{1}{2}$;
(3)当∠ACB=90°时,四边形AECF是正方形.
∵MN∥BD,
∴∠AOE=∠ACB=90°,
∴AC⊥EF,
∵四边形AECF是矩形,
∴四边形AECF是正方形,
故答案为:90°.
点评 此题主要考查了矩形和正方形的判定,以及角平分线的定义,平行线的性质,关键是掌握正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等或对角线互相垂直;
②先判定四边形是菱形,再判定这个菱形有一个角为直角或对角线相等.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B. | $\sqrt{8}÷\sqrt{2}$=4 | C. | $\sqrt{27}$=3$\sqrt{3}$ | D. | (1+$\sqrt{2})(1-\sqrt{2})=1$(1-$\sqrt{2}$)=1 |
5.关于x的分式方程$\frac{m}{x-5}$=1,下列说法正确的是( )
| A. | m<-5时,方程的解为负数 | B. | m>-5时,方程的解是正数 | ||
| C. | 方程的解是x=m+5 | D. | 无法确定 |

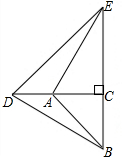 如图,△ACB和△DCE都是等腰直角三角形,点A在线段CD上,连接AE、BD.
如图,△ACB和△DCE都是等腰直角三角形,点A在线段CD上,连接AE、BD.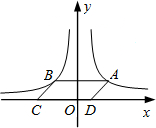 如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7.
如图,点A是反比例函数y=$\frac{4}{x}$(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-$\frac{3}{x}$(x<0)的图象于点B,以AB为边作?ABCD,其中C,D在x轴上,则?ABCD的面积为7.