Question

8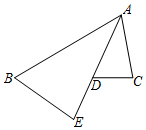．如图，已知AE 平分∠BAC，$\frac{AB}{AE}$=$\frac{AD}{AC}$．
（1）求证：∠E=∠C；
（2）若AB=9，AD=5，DC=3，求BE的长．

Answer 1

分析 （1）由AE 平分∠BAC，得到∠BAE=∠EAC，根据三角形角平分线的到来得到$\frac{AB}{AE}=\frac{AD}{AC}$，得到$\frac{AB}{AD}=\frac{AE}{AC}$，推出△ABE∽△ADC，根据相似三角形的性质即可得到结论；
（2）根据相似三角形的性质得到$\frac{AB}{AD}=\frac{BE}{DC}$，列方程即可得到结论．

解答 （1）证明：∵AE 平分∠BAC，
∴∠BAE=∠EAC，
又∵$\frac{AB}{AE}=\frac{AD}{AC}$，得到$\frac{AB}{AD}=\frac{AE}{AC}$，
∴△ABE∽△ADC，
∴∠E=∠C；

（2）解：∵△ABE∽△ADC，
∴$\frac{AB}{AD}=\frac{BE}{DC}$，
设BE=x，
∵$\frac{9}{5}=\frac{x}{3}$，
∴$x=\frac{27}{5}$，即BE=$\frac{27}{5}$．

点评 本题考查了相似三角形的判定和性质，角平分线的定义，熟练掌握相似三角形的判定和性质是解题的关键．