题目内容
18.在△ABC中,∠C=90°,AC=BC=2,将一块三角板的直角顶点放在斜边AB的中点P处,将此三角板绕点P旋转,三角板的两直角边分别交射线AC、BC于点D、E.图①②③是旋转得到的三种图形.(1)观察线段PD和PE之间有怎样的大小关系,以图②为例,加以说明.
(2)△PBE是否能成为等边三角形?若能,直接写出∠PEB的度数.若不能,请说明理由.

分析 (1)结论:PD=PE.如图②中,连接PC.只要证明△DPC≌△EPB,即可解决问题.
(2)不可能.理由:∠PBE=45°或135°.
解答 解:(1)结论:PD=PE.
理由:如图②中,连接PC.
∵∠C=90°,AC=BC,AP=PB,
∴PC=PA=PB,CP⊥AB,∠PCA=∠PCB=∠B=45°,
∵∠DPE=∠CPB=90°,
∴∠DPC=∠EPB,
在△DPC和△EPB中,
$\left\{\begin{array}{l}{∠DPC=∠EPB}\\{∠DCP=∠B}\\{PC=PB}\end{array}\right.$,
∴△DPC≌△EPB,
∴PD=PE.
(2))△PBE不可能是等边三角形.
利用:∵△ABC是等腰直角三角形,
∴∠PBE=45°或135°,
∴△PBE不可能是等边三角形.
点评 本题考查旋转变换、等腰直角三角形的性质、全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
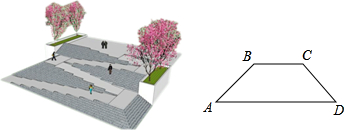
6.如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
| 坡度 | 1:20 | 1:16 | 1:12 |
| 最大高度(米) | 1.50 | 1.00 | 0.75 |
(2)求斜坡底部点A与台阶底部点D的水平距离AD.

3.由二次函数y=(x-1)2-3可知( )
| A. | 图象开口向下 | B. | 对称轴是直线x=-1 | ||
| C. | 函数最小值是3 | D. | 顶点是(1,-3) |
 如图,在楼房底部B处看热气球底部A处的仰角为60°,同时在这栋楼的顶部C处看A处的仰角为30°,已知楼高BC为30m,求此时热气球底部A处的高度.(测角仪的高度忽略不计)
如图,在楼房底部B处看热气球底部A处的仰角为60°,同时在这栋楼的顶部C处看A处的仰角为30°,已知楼高BC为30m,求此时热气球底部A处的高度.(测角仪的高度忽略不计)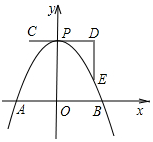 如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.
如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.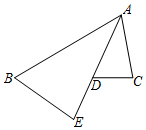 如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.
如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.