题目内容
16. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为20米(如图所示),设这个苗圃园垂直于墙的一边长为x米(1)若苗圃园的面积为108平方米,求x.
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
(3)当这个苗圃园的面积不小于72平方米时,直接写出x的取值范围.
分析 (1)根据题意可以得到关于x的方程,从而可以求得x的值;
(2)根据题意可得到面积与平行于墙的一边长的函数关系式,从而可以解答本题;
(3)根据题意可以得到相应的不等式,从而可以解答本题.
解答 解:(1)由题意可得,
x(30-2x)=108,
解得,x1=6,x2=9,
当x=6时,30-2x=18<20,
当x=9时,30-2x=12<20,
即x的值是6或9;
(2)设矩形的面积为y平方米,平行于墙的一边长为a米,
y=a($\frac{30-a}{2}$)=-$\frac{1}{2}(a-15)^{2}+\frac{225}{2}$,
∵8≤a≤20,
∴当a=15时,y取得最大值,此时y=$\frac{225}{2}$,
当a=8时,y取得最小值,此时y=88,
即平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值,最大值是$\frac{225}{2}$平方米,最小值是88平方米;
(3)由题意可得,
x(30-2x)≥72,
解得,3≤x≤12,
又∵30-2x≤20,
解得,x≥5,
∴当这个苗圃园的面积不小于72平方米时,x的取值范围是5≤x≤12.
点评 本题考查二次函数的应用、一元二次方程的应用、解不等式,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
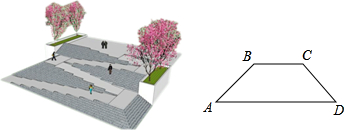
6.如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
| 坡度 | 1:20 | 1:16 | 1:12 |
| 最大高度(米) | 1.50 | 1.00 | 0.75 |
(2)求斜坡底部点A与台阶底部点D的水平距离AD.

1.下列说法正确的有( )句.
①两条射线组成的图形叫做角;
②同角的补角相等;
③若AC=BC,则C为线段AB的中点;
④线段AB就是点A与点B之间的距离;
⑤平面上有三点A、B、C,过其中两点的直线有三条或一条.
①两条射线组成的图形叫做角;
②同角的补角相等;
③若AC=BC,则C为线段AB的中点;
④线段AB就是点A与点B之间的距离;
⑤平面上有三点A、B、C,过其中两点的直线有三条或一条.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.成都市中心城区缓堵保畅“两快两射两环”工程正在紧锣密鼓地进行,此工程建成后每天能运送20多万人次,这里的200000人次有科学记数法表示为( )人次.
| A. | 2×105 | B. | 20×104 | C. | 0.2×106 | D. | 2×106 |
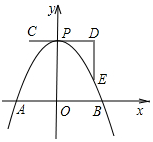 如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.
如图,一条抛物线与x轴的交点为A、B两点,其顶点P在折线C-D-E上运动.若C、D、E的坐标分别为(-1,4)、(3、4)、(3,1),点B横坐标的最小值为1,则点A横坐标的最大值为2.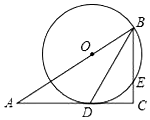 如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.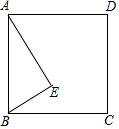 如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.
如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.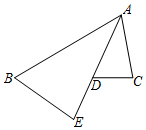 如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$.
如图,已知AE 平分∠BAC,$\frac{AB}{AE}$=$\frac{AD}{AC}$. 如图,在?ABCD中,BC=12cm,∠ABC=60°,AC⊥AB,O是AC的中点,点E,F分别从点O出发,沿射线OA和OC方向移动,速度都是每秒1cm.
如图,在?ABCD中,BC=12cm,∠ABC=60°,AC⊥AB,O是AC的中点,点E,F分别从点O出发,沿射线OA和OC方向移动,速度都是每秒1cm.