题目内容
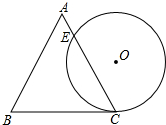 一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )
一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点:切线的性质
专题:
分析:连接OC,并过点O作OF⊥CE于F,已知OC的长度,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
解答:解:连接OC,并过点O作OF⊥CE于F,
∵△ABC为等边三角形,
∴∠ACB=60°,
∵⊙O与BC相切于点C,
∴∠OCB=90°,
∴∠OCF=30°,
∴OF=1cm,
在Rt△OFC中,
FC=
=
c,
∴CE=2FC=2
cm.
故选:B.

∵△ABC为等边三角形,
∴∠ACB=60°,
∵⊙O与BC相切于点C,
∴∠OCB=90°,
∴∠OCF=30°,
∴OF=1cm,
在Rt△OFC中,
FC=
| OC2-OF2 |
| 3 |
∴CE=2FC=2
| 3 |
故选:B.
点评:本题主要考查了切线的性质和等边三角形的性质和解直角三角形的有关知识,属于基础性题目.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
前进乡在新农村建设中为坐落于大山中的秀水村修筑通向县成的公路投资的15万元人民币,这条5公里的路在一个月内顺利完工.15万用科学记数法表示为( )
| A、1.5×10 |
| B、1.5×105 |
| C、15×104 |
| D、1.5×104 |
如图所示,阴影部分面积最大的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC的长是( )
如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC的长是( )| A、2 | B、4 | C、6 | D、8 |
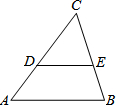 如图,DE∥AB,AC=3AD,S△ABC=5,则△CED的面积是
如图,DE∥AB,AC=3AD,S△ABC=5,则△CED的面积是 如图,B,C,D是线段AE上的三个点,已知AE=9,BD=4,求图中以A、B、C、D、E这5个点为端点的所有线段的和为
如图,B,C,D是线段AE上的三个点,已知AE=9,BD=4,求图中以A、B、C、D、E这5个点为端点的所有线段的和为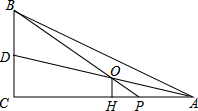 如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?
如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?