题目内容
小红、小明在一起写作业,老师布置的一道思考题引起他们的兴趣:“已知半径为10cm的⊙O中有两条平行弦AB、CD,且AB=12cm,CD=16cm,求AB、CD间的距离.”小红得到的结果是“两平行弦之间的距离为14cm”,小明得到的结果是“两平行弦之间的距离为2cm”.你认为他们俩谁对?为什么?说明理由.
考点:垂径定理,勾股定理
专题:分类讨论
分析:作OE⊥AB于E,OE交CD于F,连结OA、OC,如图,根据平行线的性质得EF⊥CD,根据垂径定理得AE=
AB=6,CF=
CD=8,再根据勾股定理,在Rt△AOE中计算出OE=8,在Rt△COF中计算出OF=6,然后分类讨论:当圆心O在AB与CD之间时,如图1,EF=OE+OF;当圆心O不在AB与CD之间时,如图2,EF=OE-OF,最后把OE与OF的值代入计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:他们都不对,两平行弦之间的距离为2cm或14cm.
理由如下:OE⊥AB于E,OE交CD于F,连结OA、OC,如图,
∵AB∥CD,
∴EF⊥CD,
∴AE=BE=
AB=6,CF=DF=
CD=8,
在Rt△AOE中,∵OA=10,AE=6,
∴OE=
=8,
在Rt△COF中,∵OC=10,CE=8,
∴OF=
=6,
当圆心O在AB与CD之间时,如图1,

EF=OE+OF=8+6=14(cm);
当圆心O不在AB与CD之间时,如图2,

EF=OE-OF=8-6=2(cm),
综上所述,AB、CD间的距离为2cm或14cm.
理由如下:OE⊥AB于E,OE交CD于F,连结OA、OC,如图,
∵AB∥CD,
∴EF⊥CD,
∴AE=BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOE中,∵OA=10,AE=6,
∴OE=
| OA2-AE2 |
在Rt△COF中,∵OC=10,CE=8,
∴OF=
| OC2-CF2 |
当圆心O在AB与CD之间时,如图1,

EF=OE+OF=8+6=14(cm);
当圆心O不在AB与CD之间时,如图2,

EF=OE-OF=8-6=2(cm),
综上所述,AB、CD间的距离为2cm或14cm.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
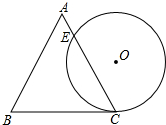 一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )
一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
 利用圆规和直尺分别作圆内接正三角形和圆内接正四边形.
利用圆规和直尺分别作圆内接正三角形和圆内接正四边形.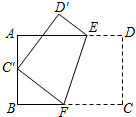 如图,将矩形ABCD沿EF折叠,使顶点C落在AB边的中点c,上.若AB=6,BC=9,则BF的长为
如图,将矩形ABCD沿EF折叠,使顶点C落在AB边的中点c,上.若AB=6,BC=9,则BF的长为 如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=
如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=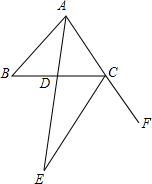 如图,已知∠ABC=31°,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为
如图,已知∠ABC=31°,又△BAC的角平分线AE与∠BCA的外角平分线CE相交于E点,则∠AEC为
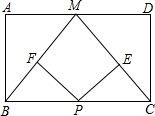 如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.
如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.