题目内容
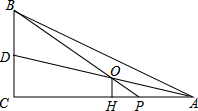 如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?
如图,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若AD平分∠BAC,且AD与BP相交于点O,OH⊥AC,计算线段OH的长度?考点:相似三角形的判定与性质
专题:
分析:由条件可求得BC=PC=6,则△PHO和△PCB都是等腰直角三角形,利用角平分线可求得CD,再利用△AHO∽△ACD可求得OH.
解答:解:
∵∠C=90°,AC=8,AB=10,
∴BC=6,
又AP=2,∴CP=AC-AP=6,
∴BC=CP,
即△BCP为等腰直角三角形,
∴OH⊥AC,
∴OH∥BC,
∴△PHO为等腰直角三角形,
设OH=x,则PH=x,AH=x+2,
∵AD平分∠BAC,
∴
=
=
,且BD+CD=6,
∴CD=
,
∵OH∥BC,
∴△AHO∽△ACD,
∴
=
,
即
=
,解得x=1,
即OH=1.
∵∠C=90°,AC=8,AB=10,
∴BC=6,
又AP=2,∴CP=AC-AP=6,
∴BC=CP,
即△BCP为等腰直角三角形,
∴OH⊥AC,
∴OH∥BC,
∴△PHO为等腰直角三角形,
设OH=x,则PH=x,AH=x+2,
∵AD平分∠BAC,
∴
| BD |
| CD |
| AB |
| AC |
| 10 |
| 8 |
∴CD=
| 8 |
| 3 |
∵OH∥BC,
∴△AHO∽△ACD,
∴
| AH |
| AC |
| OH |
| CD |
即
| 2+x |
| 8 |
| x | ||
|
即OH=1.
点评:本题主要考查相似三角形的判定和性质,利用角平分线的性质求得CD的长是解题的关键.注意方程思想的应用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
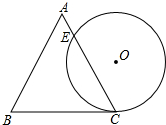 一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )
一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
某钢铁厂1月份生产某种钢材5万吨,3月份生产这种钢材7.2万吨,设平均每月增长的百分率为x,则根据题意可列方程为( )
| A、5(1+x)=7.2 |
| B、5(1+x2)=7.2 |
| C、5(1+x)2=7.2 |
| D、7.2(1+x)2=5 |
 如图,菱形ABCD的周长40cm,它的一条对角线BD长10cm.
如图,菱形ABCD的周长40cm,它的一条对角线BD长10cm. 利用圆规和直尺分别作圆内接正三角形和圆内接正四边形.
利用圆规和直尺分别作圆内接正三角形和圆内接正四边形.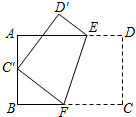 如图,将矩形ABCD沿EF折叠,使顶点C落在AB边的中点c,上.若AB=6,BC=9,则BF的长为
如图,将矩形ABCD沿EF折叠,使顶点C落在AB边的中点c,上.若AB=6,BC=9,则BF的长为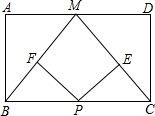 如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.
如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.