题目内容
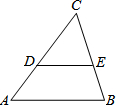如图，DE∥AB，AC=3AD，S△ABC=5，则△CED的面积是考点：相似三角形的判定与性质
专题：
分析：由平行可得△CDE∽△CAB，且可得
=
，再利用相似三角形的面积比等于相似比的平方，可求得△CED的面积．
| CD |
| CA |
| 2 |
| 3 |
解答：解：
∵AC=3AD，
∴CD=2AD，
∴
=
，
∵DE∥AB，
∴△CDE∽△CAB，
∴
=（
）2=（
）2=
，且S△ABC=5，
∴
=
，
∴S△CED=
，
故答案为：
．
∵AC=3AD，
∴CD=2AD，
∴
| CD |
| CA |
| 2 |
| 3 |
∵DE∥AB，
∴△CDE∽△CAB，
∴
| S△CDE |
| S△CAB |
| CD |
| CA |
| 2 |
| 3 |
| 4 |
| 9 |
∴
| S△CED |
| 5 |
| 4 |
| 9 |
∴S△CED=
| 20 |
| 9 |
故答案为：
| 20 |
| 9 |
点评：本题主要考查相似三角形的判定和性质，利用条件求得相似比是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
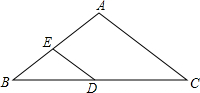如图，在△ABC中，AB=AC，∠B=40°，D为BC上一点，DE∥AC交AB于E，则∠BED的度数为（ ）| A、140° | B、80° |
| C、100° | D、70° |
如图，在平面直角坐标系中，A、B、C三点的坐标分别为（3，0）、（1，
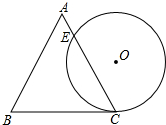一个边长为4cm的等边三角形ABC与半径为2cm⊙O如图放置，⊙O与BC相切于点C，⊙O与AC相交于点E，则CE的长为（ ）A、
| ||
B、2
| ||
C、
| ||
D、2
|
利用圆规和直尺分别作圆内接正三角形和圆内接正四边形．