题目内容
已知△ABC中,点E为AB边的中点,将△AEC沿CE所在直线折叠得△A′EC,BF∥AC交直线A′C于F,如图(1)当△ACB=90°,易证AC=CF+BF.
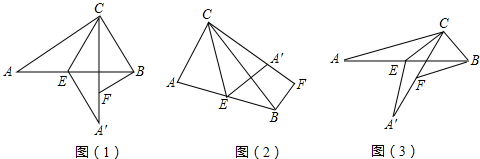
(1)若∠ACB为任意角,如图(2)、图(3),猜想线段AC、CF、BF之间有怎样的数量关系并证明图(3)结论:
(2)若∠CBF=60°,BF=4,BC=6,则AC的长为 .

(1)若∠ACB为任意角,如图(2)、图(3),猜想线段AC、CF、BF之间有怎样的数量关系并证明图(3)结论:
(2)若∠CBF=60°,BF=4,BC=6,则AC的长为
考点:全等三角形的判定与性质,翻折变换(折叠问题)
专题:
分析:(1)连接A′B,易证∠FBA=∠A,可得∠FBA=∠EA′F,易证∠EA′B=∠EBA′,即可证明∠FBA′=∠FA′B,即可解题;
(2)根据余弦定理可以求得CF的长,根据(1)中结论即可解题.
(2)根据余弦定理可以求得CF的长,根据(1)中结论即可解题.
解答:(1)证明:连接A′B,

∵BF∥AC,
∴∠FBA=∠A,
∵∠A=∠EA′F(折叠),
∴∠FBA=∠EA′F,
∵E为AB中点,
∴AE=EB,
∵A'E=AE,
∴A'E=EB,
∴∠EA′B=∠EBA′,
∵∠EBF=∠EA′F,∠EA′B-∠EA′F=∠EBA′-∠EBF,
∴∠FBA′=∠FA′B.
∴FB=FA′,
∴FB+CF=AC;
(2)解:∵∠CBF=60°,BF=4,BC=6,CF2=BF2+BC2-2BC•BFcos∠CBF,
∴CF=2
,
∴AC=CF+BF=2
+4.
故答案为 2
+4.

∵BF∥AC,
∴∠FBA=∠A,
∵∠A=∠EA′F(折叠),
∴∠FBA=∠EA′F,
∵E为AB中点,
∴AE=EB,
∵A'E=AE,
∴A'E=EB,
∴∠EA′B=∠EBA′,
∵∠EBF=∠EA′F,∠EA′B-∠EA′F=∠EBA′-∠EBF,
∴∠FBA′=∠FA′B.
∴FB=FA′,
∴FB+CF=AC;
(2)解:∵∠CBF=60°,BF=4,BC=6,CF2=BF2+BC2-2BC•BFcos∠CBF,
∴CF=2
| 7 |
∴AC=CF+BF=2
| 7 |
故答案为 2
| 7 |
点评:本题考查了等腰三角形底角相等的性质,考查了余弦定理的运用,考查了折叠的性质,本题中求证AF=BF是解题的关键.

练习册系列答案
相关题目