题目内容

己知：x2+y2+2x-4y=5，求x+y的值．
考点：配方法的应用,非负数的性质：偶次方
专题：计算题
分析：已知等式移项变形，配方后利用非负数的性质求出x与y的值，即可求出x+y的值．
解答：解：已知等式变形得：（x+1）2+（y-2）2=0，
可得x+1=0，y-2=0，
解得：x=-1，y=2，
则x+y=-1+2=1．
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
已知下列方程：①x-2=
1
x
；②0.2x=1；③
x
3
=x-3；④x2-4-3x=0；⑤x=0；⑥x-y=6；其中一元一次方程是
 
．
化简：
（1）
12
2

（2）
3
6
．
在Rt△ABC中，∠C=90°
（1）已知∠A，c，写出解Rt△ABC的过程；
（2）已知∠A，a，写出解Rt△ABC的过程；
（3）已知a，c，写出解Rt△ABC的过程．
已知△ABC中，点E为AB边的中点，将△AEC沿CE所在直线折叠得△A′EC，BF∥AC交直线A′C于F，如图（1）当△ACB=90°，易证AC=CF+BF．

（1）若∠ACB为任意角，如图（2）、图（3），猜想线段AC、CF、BF之间有怎样的数量关系并证明图（3）结论：
（2）若∠CBF=60°，BF=4，BC=6，则AC的长为
 
．
新规定这样一种运算法则：a※b=a2+2ab，例如3※（-2）=32+2×3×（-2）=-3．
（1）若1※x=3，求x的值；
（2）若（-2）※x=-2+x，求x的值．
已知代数式x+y的值是3，则代数式2x+2y+1的值是
 
．
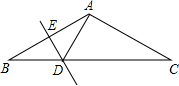如图，AB=AC，∠BAC=120°，AB的垂直平分线交BC于点D，交AB于点E，则∠ADC的度数是（　　）
A、30°B、60°
C、45°D、65°
已知a、b、c为实数，
a+b
ab
=6，
b+c
bc
=8，
a+c
ac
=10，求
ab+bc+ca
abc
的值．（提示：裂项法
a+b
ab
=
a
ab
+
b
ab
=
1
b
+
1
a
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网