题目内容
某高速公路的建设正在紧张地进行,现有大量的沙石需要运输.某车队有载重量为8吨、10吨的卡车共10辆,全部车辆运输一次能运输92吨沙石.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,该车队需要一次运输沙石140吨,为了完成任务,该车队准备新增购这两种卡车共5辆,则需新增购这两种卡车各多少辆?
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,该车队需要一次运输沙石140吨,为了完成任务,该车队准备新增购这两种卡车共5辆,则需新增购这两种卡车各多少辆?
考点:一元一次方程的应用
专题:
分析:(1)设载重8吨的卡车有x辆,则载重10吨的卡车有(10-x)辆.等量关系为:某车队有载重量为8吨、10吨的卡车共10辆,全部车辆运输一次能运输92吨沙石;
(2)设需新增购载重8吨的卡车y辆,则购载重10吨的卡车(5-y)辆,根据“该车队需要一次运输沙石140吨”列出方程.
(2)设需新增购载重8吨的卡车y辆,则购载重10吨的卡车(5-y)辆,根据“该车队需要一次运输沙石140吨”列出方程.
解答:解:(1)设载重8吨的卡车有x辆,则载重10吨的卡车有(10-x)辆.?
根据题意得:8x+10(10-x)=92,
解之得:x=4,
10-x=6.
答:该车队有载重8吨卡车4辆,10吨卡车6辆;
(2)设需新增购载重8吨的卡车y辆,则购载重10吨的卡车(5-y)辆.
根据题意得:8(4+y)+10(6+5-y)=140,
解得:y=1,
5-y=4.
答:需新增购载重8吨的卡车1辆,载重10吨的卡车4辆.
根据题意得:8x+10(10-x)=92,
解之得:x=4,
10-x=6.
答:该车队有载重8吨卡车4辆,10吨卡车6辆;
(2)设需新增购载重8吨的卡车y辆,则购载重10吨的卡车(5-y)辆.
根据题意得:8(4+y)+10(6+5-y)=140,
解得:y=1,
5-y=4.
答:需新增购载重8吨的卡车1辆,载重10吨的卡车4辆.
点评:此题主要考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
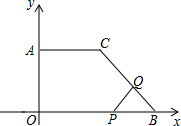 如图,直角坐标系中有直角梯形AOBC,点A在y轴正半轴上,点B在x轴正半轴上,AC∥OB,AC=6cm,AO=8cm,OB=12cm.
如图,直角坐标系中有直角梯形AOBC,点A在y轴正半轴上,点B在x轴正半轴上,AC∥OB,AC=6cm,AO=8cm,OB=12cm.