题目内容
15.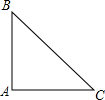 在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
在△ABC中,∠BAC=90°,AB=AC=4,在△ABC的外部,以AB为直角边作等腰直角△ABD,连接CD,则△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
分析 分情况讨论,①以A为直角顶点,向外作等腰直角三角形DAC;②以B为直角顶点,向外作等腰直角三角形ADB.分别画图,即可得到结论.
解答 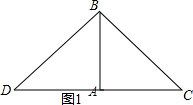 解:①如图1,以A为直角顶点,向外作等腰直角三角形DAB,
解:①如图1,以A为直角顶点,向外作等腰直角三角形DAB,
∵∠DAB=90°,且AD=AB=4,
∴BD=BC=4$\sqrt{2}$,
∴△BCD的周长=8$\sqrt{2}$+8;
②如图2,以B为直角顶点,向外作等腰直角三角形ABD,
,连接CD,过点D作DE⊥AC,交AC的延长线于E.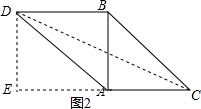
∵△ABC是等腰直角三角形,∠ACD=90°,
∴∠DAE=45°,
又∵DE⊥CE,
∴∠DEC=90°,
∴∠ADE=45°,
∴AE=DE=4,
∴CE=8,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=4$\sqrt{5}$,
∴△BCD的周长为4$\sqrt{5}$+4$\sqrt{2}$+4;
故答案为:4$\sqrt{5}$+4$\sqrt{2}$+4或8$\sqrt{2}$+8.
点评 本题考查了等腰直角三角形的性质、勾股定理等知识,解题时注意分类讨论,不要漏掉所有可能的情况.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
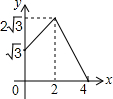
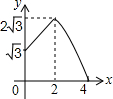
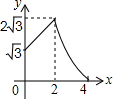
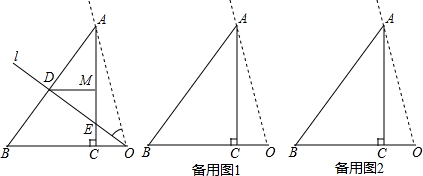
 如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,E是BC的中点,点P、Q分别从A、E出发,沿着四边形的边向D点移动,移动时始终保持PQ∥AE,设△BPQ的面积是y,AP=x,则y关于x的函数图象大致是( )
如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,E是BC的中点,点P、Q分别从A、E出发,沿着四边形的边向D点移动,移动时始终保持PQ∥AE,设△BPQ的面积是y,AP=x,则y关于x的函数图象大致是( )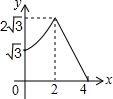
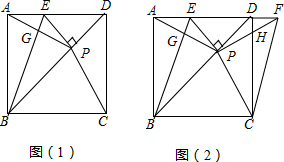
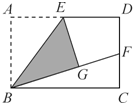 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
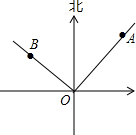 如图,点O表示学校,点A表示小明的家,点B表示小红的家,其中∠AOB=90°,小明的家在学校的北偏东40°的方向上,那么小红的家在学校的北偏西50°的方向上.
如图,点O表示学校,点A表示小明的家,点B表示小红的家,其中∠AOB=90°,小明的家在学校的北偏东40°的方向上,那么小红的家在学校的北偏西50°的方向上.